What is Quick Sort?
First, let’s look at the terms used in quick sort:
| Term | Description |
|---|---|
| Pivot | Refers to the center of sorting. Read as Pivot. |
| Low | Points to the leftmost point excluding Pivot. |
| High | Points to the rightmost point excluding Pivot. |
| Left | Points to the leftmost point of sorted elements |
| Right | Points to the rightmost point of elements to sort. |
Examining it in more detail through the example diagram below. Here, pivot is < element 6 > located at the leftmost position.
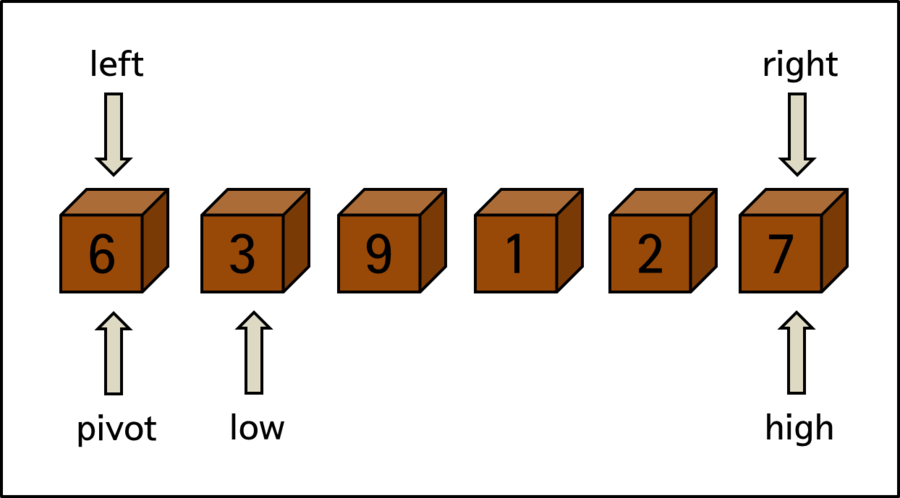
low is < element 3 > and moves to the right while proceeding with sorting. Conversely, high is < element 7 > and moves to the left while proceeding with sorting. Of course, low and high don’t move one space at a time alternately, but proceed independently.
Quick Sort Process
The rules are simple. high finds values smaller than pivot, and conversely, low finds values larger than pivot. When values matching the conditions are found, high and low exchange the values they found.
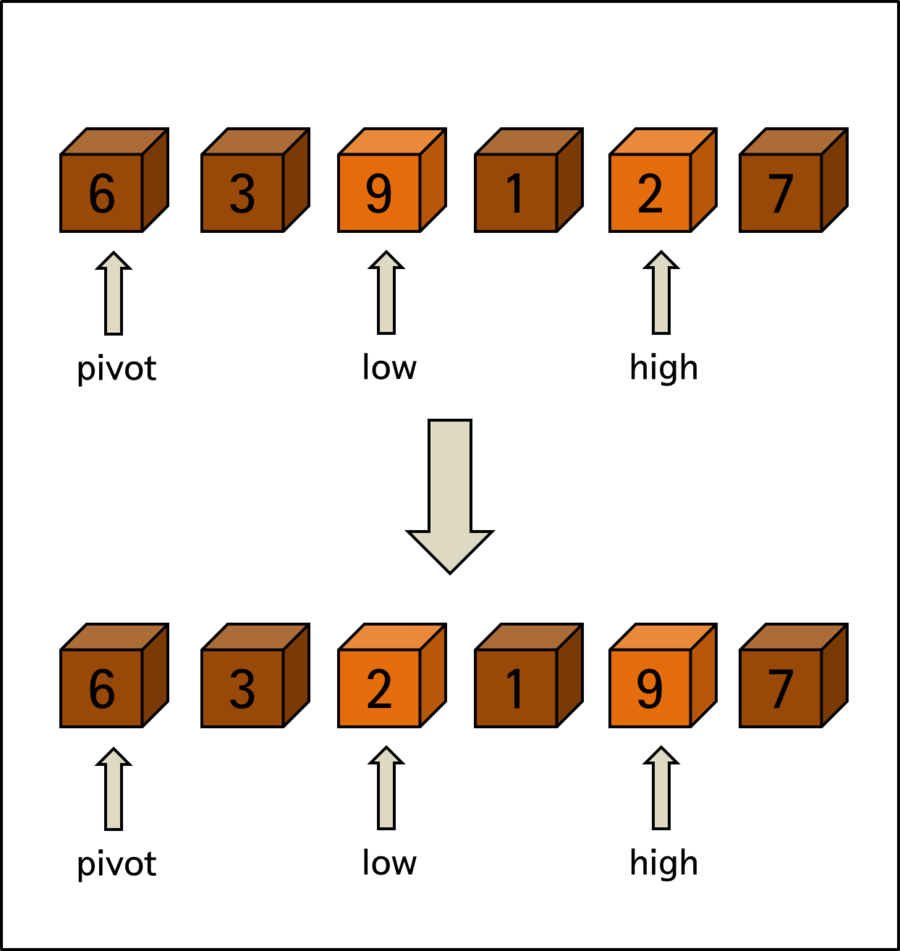
This is the state after < Exchange 1 >. < element 2 > found by high and < element 9 > found by low have been exchanged. After high and low are exchanged, high continues to move left to find values larger than pivot, and low continues to move right to find values smaller than pivot.
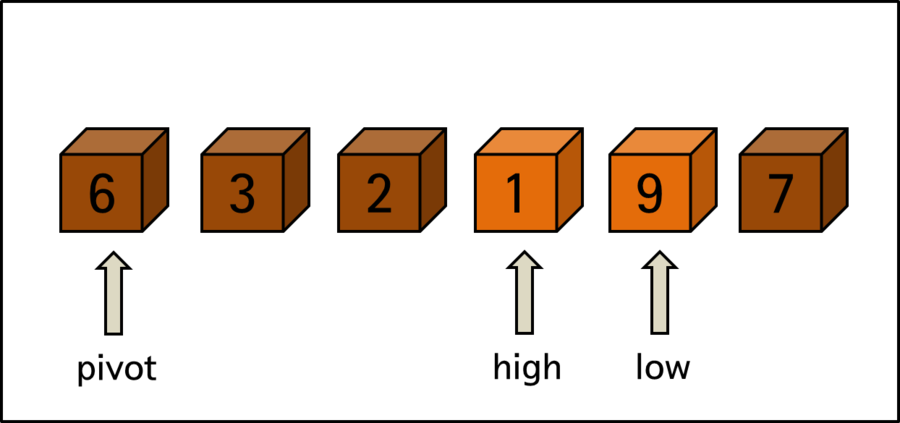
high found < element 1 > which is smaller than pivot < element 6 >, and low found < element 9 > which is larger than pivot. However, when high and low cross each other like now, they don’t exchange values. The reason is that it means the movement and exchange of high and low are complete.
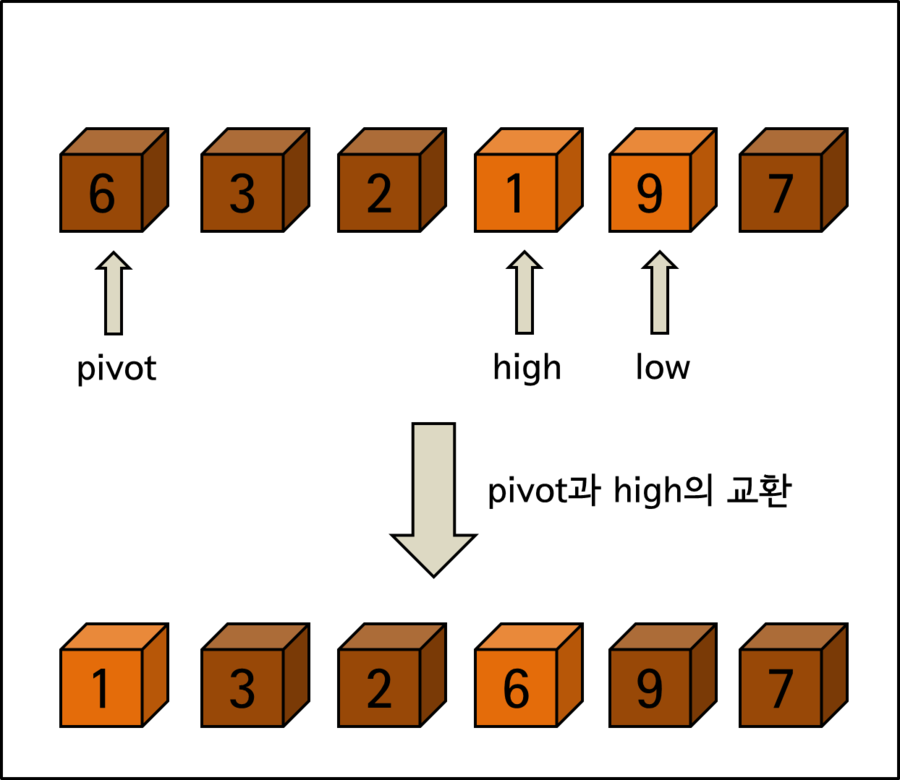
Looking at the position of the moved pivot value, it’s located at the fourth position from the front. Since there are only 6 elements to sort, some of you may have noticed, but through the exchange just now, < element 6 > has found its sorting position.
Afterward, the above process is repeated again, divided into left and right areas based on < element 6 > which has found its sorting position.
Quick Sort Implementation
Examining the above quick sort process through source code:
#include <stdio.h>
#include <stdlib.h>
void Swap(int arr[], int firstIndex, int secondIndex)
{
int temp = arr[firstIndex];
arr[firstIndex] = arr[secondIndex];
arr[secondIndex] = temp;
}
int Partition(int arr[], int left, int right)
{
// Set pivot position to the leftmost element.
int pivot = arr[left];
int low = left + 1;
int high = right;
// Until low and high don't cross
while (low <= high)
{
// low finds values larger than pivot.
while (pivot >= arr[low] && low <= right)
low++;
// high finds values smaller than pivot.
while (pivot <= arr[high] && high >= (left+1))
high--;
// If low and high haven't crossed, exchange the two values.
if (low <= high) Swap(arr, low, high);
}
// Exchange pivot and high.
Swap(arr, left, high);
return high;
}
void QuickSort(int arr[], int left, int right)
{
if (left <= right)
{
// Divide.
int pivot = Partition(arr, left, right);
// Sort elements located on the left.
QuickSort(arr, left, pivot - 1);
// Sort elements located on the right.
QuickSort(arr, pivot + 1, right);
}
}
int main(void)
{
int arr[] = { 6, 3, 9, 1, 2, 7 };
int index = 0;
int arrSize = (sizeof(arr) / sizeof(int));
QuickSort(arr, 0, arrSize - 1);
for (index = 0; index < arrSize; index++)
printf("%d ", arr[index]);
return 0;
}
Examining each condition of the loop that increments low’s value and decrements high’s value. First, the increment condition for low:
/* Condition to find values larger than pivot */
1) pivot >= arr[low]
/* If low's value becomes larger than right's value, it's considered to exceed the maximum index range of the array */
2) low <= right
Next, the decrement condition for high.
/* Condition for high to find values smaller than pivot */
1) pivot <= arr[high]
/* If high's value becomes smaller than (left + 1), it's considered to point to pivot or exceed the minimum index of the array */
2) high >= (left + 1)
About Pivot Position
As done in this post, when specifying the leftmost element as pivot, there can be an issue of uneven division. Unlike the example, if pivot is in the middle, sorting elements are divided evenly. For this reason, specifying pivot position as the middle element shows the best performance.
That is, since finding the median value by searching all elements takes time, pivot is determined using the median value among left end, center, and right end.
What is the Performance of Quick Sort?
The comparison operations that occur in the process of pivot finding its position occur n times, the number of elements. Of course, due to pivot itself, comparison operations proceed one less than n times, but this is ignored.
We should also examine how many stages the division consists of. Let’s assume there are 31 elements. Assuming pivot position is ideally determined to be in the middle, in the first division process, all elements are divided into two groups of 15 each. And in the next division, they’re divided into 7 each, totaling 4 areas. These areas are divided again into 3 elements each, totaling 8 areas, and finally divided into 1 each, totaling 16 areas.
When assuming the number of divisions as k, the number of elements n and k can be expressed as \(k=\log _{ 2 }{ n }\). That is, quick sort’s comparison count is \(n\log _{ 2 }{ n }\) and expressed in Big-O notation is \(O(n\log _{ 2 }{ n } )\).
However, if elements are already sorted and pivot is the smallest value (like in the example), then \(k=n\). That is, in the worst case, \(O({ n }^{ 2 })\) holds.