What is Merge Sort?

Merge sort proceeds through processes called Divide, Conquer, and Combine. Instead of sorting elements at once, it divides elements in half and divides them again in half to sort.

The entire process can be expressed as follows:

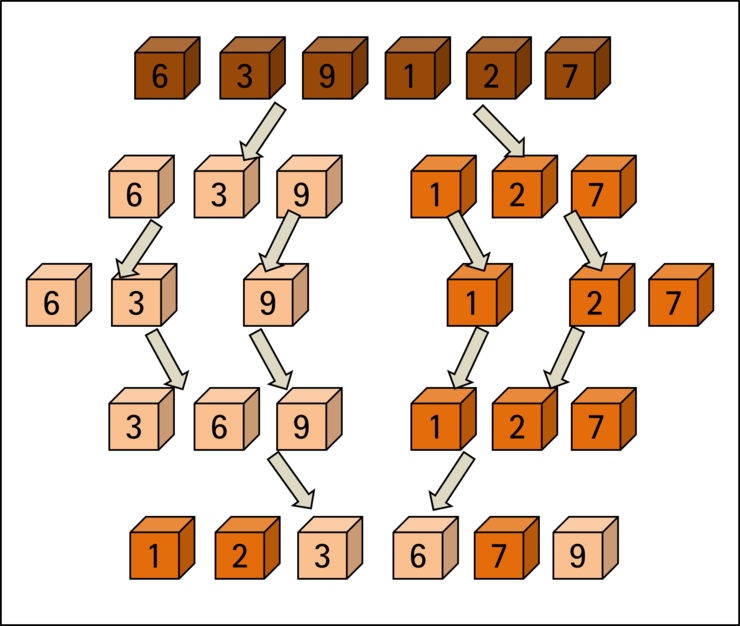
Merge Sort Process

Examining each step of the entire sorting process above in more detail. When sorting elements are divided in half, the left area is labeled as left, the right area as right, and Start and End are labeled at the beginning and end of each.

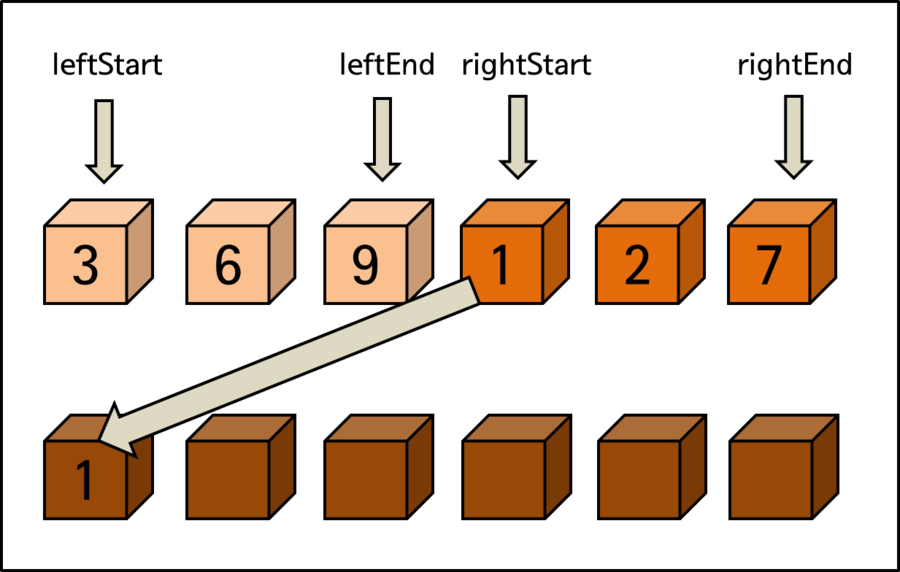
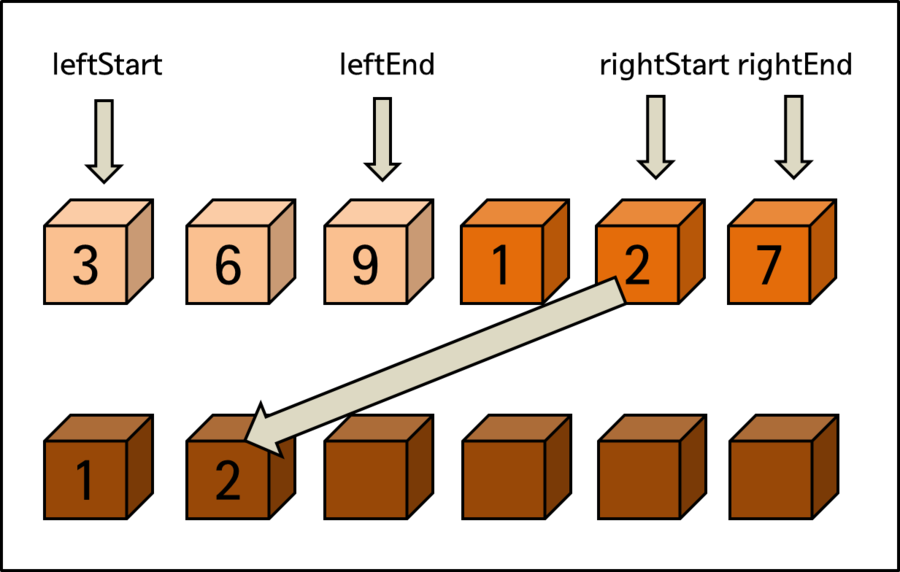
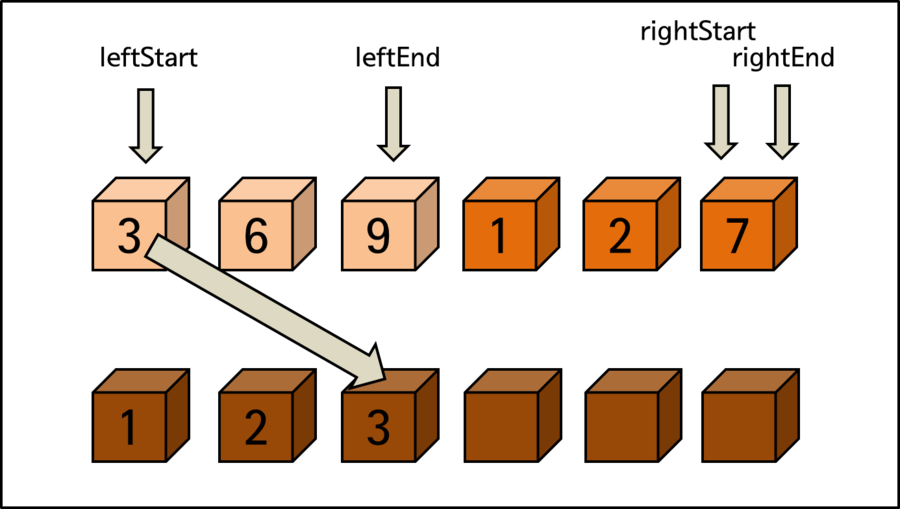
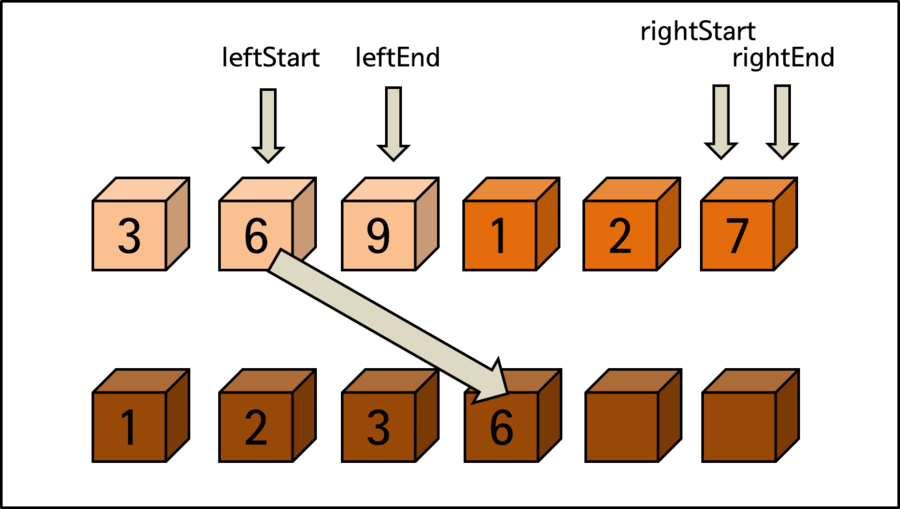
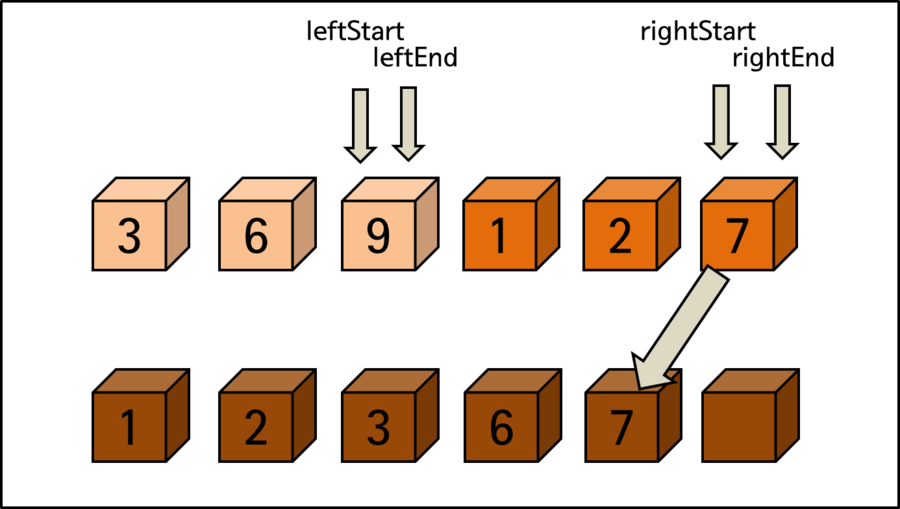
After the last comparison process, rightStart, which is the start of the right area, becomes a position beyond rightEnd, which is the end of the right. This means that further comparisons for sorting are meaningless.

Merge Sort Implementation

Examining the above process through source code:

#include <stdio.h>
#include <stdlib.h>

void Merge(int arr[], int left, int mid, int right)
{
    int leftStart = left;
    int leftEnd = mid;
    int rightStart = mid + 1;
    int rightEnd = right;
    int index = 0;
 
    // Dynamically allocate array containing merged results
    int* sortedArr = (int*)malloc(sizeof(int)*(right + 1));
    int sortedArrIndex = left;

    while ((leftStart <= leftEnd) && (rightStart <= rightEnd)) {
        if (arr[leftStart] > arr[rightStart]) {
            sortedArr[sortedArrIndex] = arr[rightStart++];
        }
        else { 
            sortedArr[sortedArrIndex] = arr[leftStart++];
        }
        sortedArrIndex++;
    }
    
    // If all of the front part of the array has been moved to the sorted array
    if (leftStart > leftEnd) {
        // Move remaining data in the back part of the array as is.
        for (index = rightStart; index <= rightEnd; index++) {
            sortedArr[sortedArrIndex++] = arr[index];
        }
    }

    // If all of the back part of the array has been moved to the sorted array
    else {
        // Move remaining data in the front part of the array as is.
        for (index = leftStart; index <= leftEnd; index++) {
            sortedArr[sortedArrIndex++] = arr[index];
        }
    }

    for (index = left; index <= right; index++)
        arr[index] = sortedArr[index];

    free(sortedArr);
}

void MergeSort(int arr[], int left, int right)
{
    int mid;

    // If left is smaller, it can be divided further
    if (left < right) {
        // Calculate midpoint
        mid = (left + right) / 2;
        
        // Sort data from left to mid
        MergeSort(arr, left, mid);

        // Sort data from mid+1 to right
        MergeSort(arr, mid + 1, right);

        // Merge the two sorted arrays
        Merge(arr, left, mid, right);
    }
}

int main(void)
{
    int arr[] = { 6, 3, 9, 1, 2, 7 };
    int index = 0;
    int arrSize = (sizeof(arr) / sizeof(int));

    MergeSort(arr, 0, arrSize-1);

    for (index = 0; index < arrSize; index++)
        printf("%d ", arr[index]);
 
    return 0;
}

What is the Performance of Merge Sort?

Consider when merging < 3, 6, 9 > and < 1, 2, 7 > as one group in the above process:

• 1) Compare 3 and 1. After comparison operation, move 1 to sorted array.
• 2) Compare 3 and 2. After comparison operation, move 2 to sorted array.
• 3) Compare 3 and 7. After comparison operation, move 3 to sorted array.
• 4) Compare 6 and 7. After comparison operation, move 6 to sorted array.
• 5) Compare 9 and 7. After comparison operation, move 7 to sorted array.
• Comparison operation of if-else statement to move remaining < 9 > to sorted array

In this way, when comparison operations proceed until one element remains, it has n, the maximum number of operations. For merge sort, regarding the number of elements n to sort and the number of merge processes k, the equation \(k=\log _{ 2 }{ n }\) holds. That is, expressing merge sort’s comparison operations in Big-O notation is \(O(n\log _{ 2 }{ n } )\).

Looking closely, there are also operations where elements are moved during the merge process. Movement occurs once in the ‘process of merging elements into a temporary array’ and once each in the ‘process of moving all elements stored in the temporary array back to their original positions’.

That is, the number of operations due to element movement can be viewed as \(2n\log _{ 2 }{ n }\) regardless of worst, average, and best cases, but since the constant 2 in Big-O notation can be ignored, the final Big-O expression can be said to be \(O(n\log _{ 2 }{ n } )\).

Merge Sort and Quick Sort

Merge sort and quick sort are good sorting algorithms to compare.

Merge sort is a Bottom-Up method that sorts small groups and then merges them into larger groups. On the other hand, quick sort is a Top-Down method where operations proceed from large groups to small groups.

Also, quick sort doesn’t require additional storage space and performs sorting only through internal exchanges, but merge sort uses additional storage space to proceed with sorting.

In terms of performance, merge sort guarantees nlogn sorting time, and has almost the same execution time because there’s time to rearrange positions, but quick sort is n, the number of elements, in the best case, and can be up to n squared in the worst case.

Despite these differences, both sorting methods are based on divide & conquer algorithms that divide areas for processing.