합병 정렬이란 무엇일까?
합병 정렬은 분할(Divide), 정복(Conquer), 결합(Combine)이라는 과정으로 진행됩니다. 요소들을 한 번에 정렬하는 것이 아닌 요소들을 반으로 나누고 이를 또 반으로 나누어 정렬하는 것이지요.
전체 과정을 보면 아래와 같이 표현할 수 있습니다.
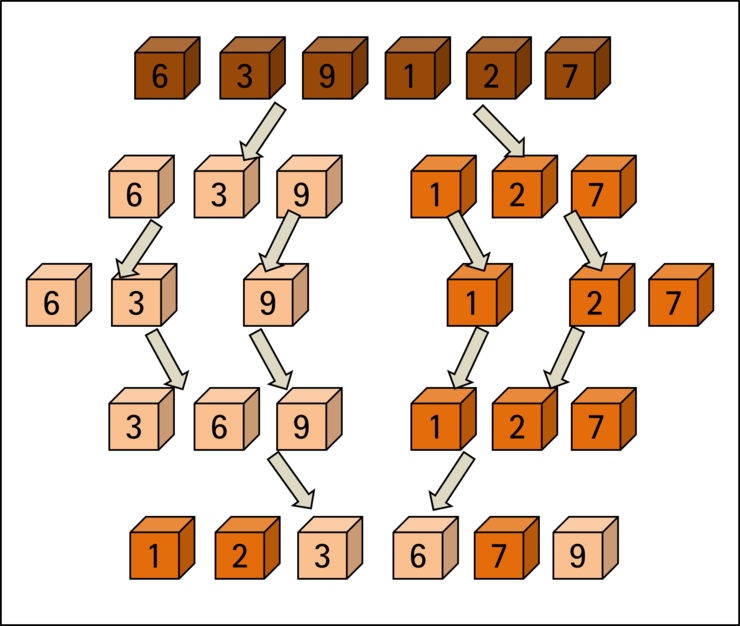
합병 정렬 진행
위의 전체 정렬 과정을 조금 더 자세히 각 단계마다 살펴봅시다. 정렬 요소들을 반으로 나누었을 때 왼쪽 영역을 left, 오른쪽 영역을 right로 표기하고 각각의 시작과 끝에 Start, End로 표기했습니다.
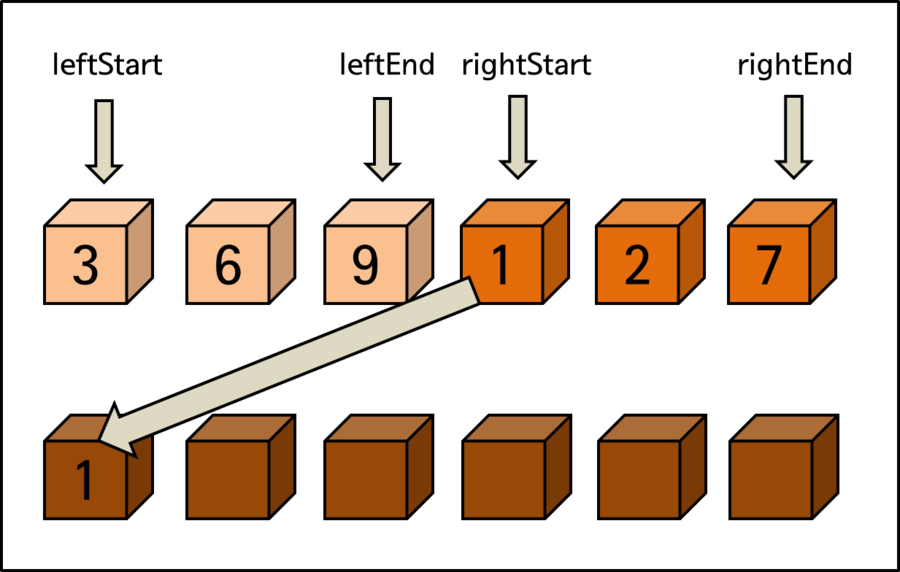
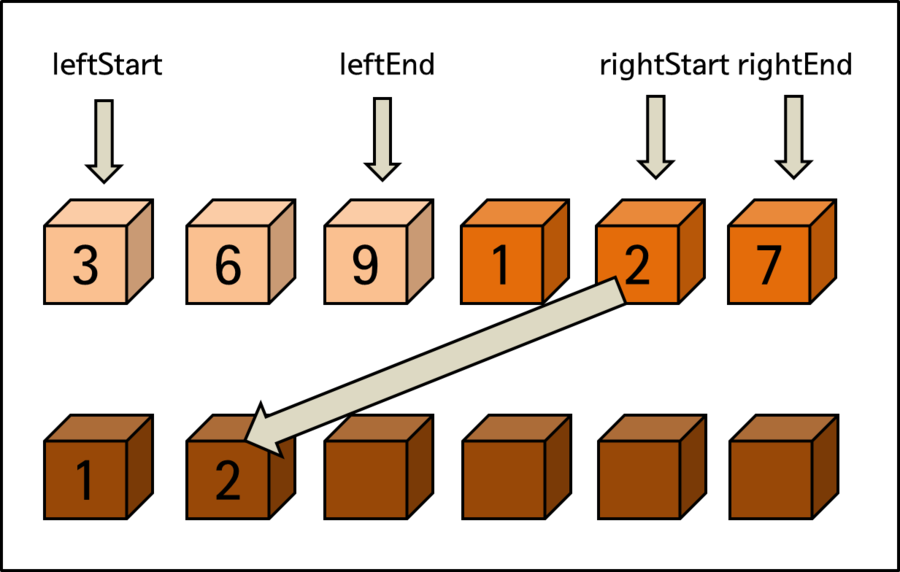
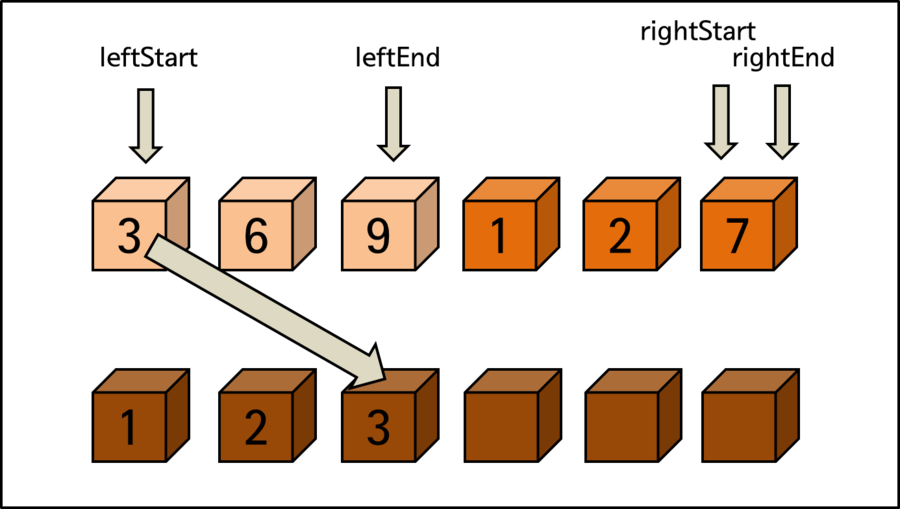
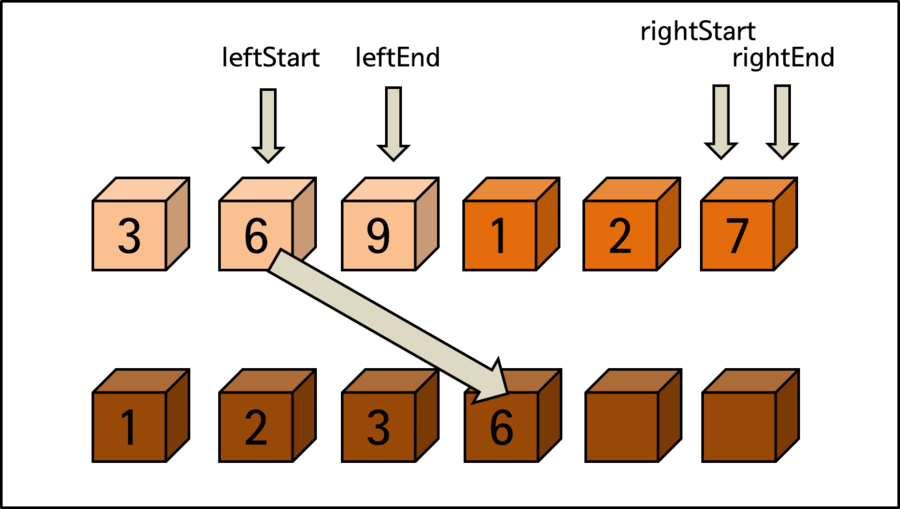
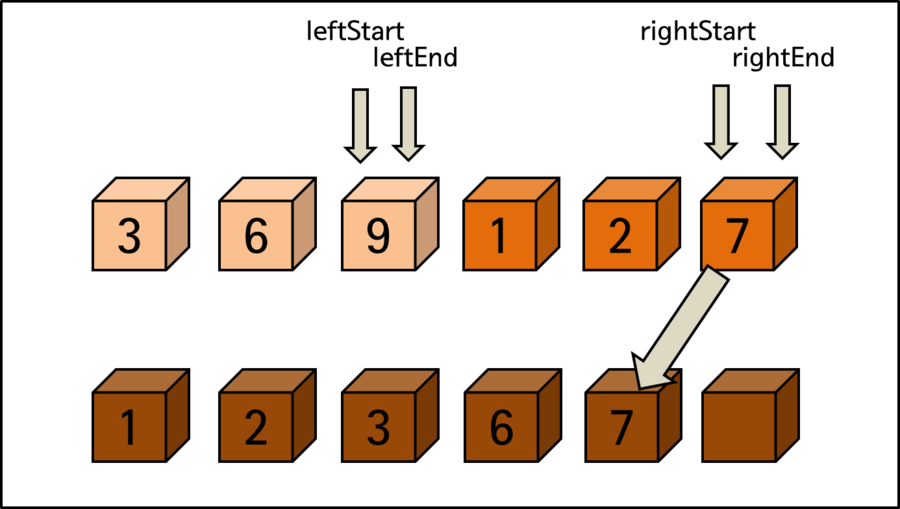
마지막 비교 과정 이후에 오른쪽 영역의 시작인 rightStart는 오른쪽의 끝인 rightEnd를 넘어서는 위치가 됩니다. 이는 더 이상의 정렬을 위한 비교는 의미가 없다는 뜻입니다.
합병 정렬 구현
위 과정을 소스 코드를 통해 살펴봅시다.
#include <stdio.h>
#include <stdlib.h>
void Merge(int arr[], int left, int mid, int right)
{
int leftStart = left;
int leftEnd = mid;
int rightStart = mid + 1;
int rightEnd = right;
int index = 0;
// 합병한 결과를 담은 배열 동적 할당
int* sortedArr = (int*)malloc(sizeof(int)*(right + 1));
int sortedArrIndex = left;
while ((leftStart <= leftEnd) && (rightStart <= rightEnd)) {
if (arr[leftStart] > arr[rightStart]) {
sortedArr[sortedArrIndex] = arr[rightStart++];
}
else {
sortedArr[sortedArrIndex] = arr[leftStart++];
}
sortedArrIndex++;
}
// 배열의 앞부분이 모두 정렬된 배열에 옮겨졌다면
if (leftStart > leftEnd) {
// 배열의 뒷부분에 남은 데이터를 그대로 옮긴다.
for (index = rightStart; index <= rightEnd; index++) {
sortedArr[sortedArrIndex++] = arr[index];
}
}
// 배열의 뒷부분이 모두 정렬된 배열에 옮겨졌다면
else {
// 배열의 앞부분에 남은 데이터를 그대로 옮긴다.
for (index = leftStart; index <= leftEnd; index++) {
sortedArr[sortedArrIndex++] = arr[index];
}
}
for (index = left; index <= right; index++)
arr[index] = sortedArr[index];
free(sortedArr);
}
void MergeSort(int arr[], int left, int right)
{
int mid;
// left가 더 작은 경우는 더 나눌 수 있는 경우
if (left < right) {
// 중간 지점 계산
mid = (left + right) / 2;
// left부터 mid까지의 데이터 정렬
MergeSort(arr, left, mid);
// mid+1부터 right까지의 데이터 정렬
MergeSort(arr, mid + 1, right);
// 정렬된 두 배열을 합병하기
Merge(arr, left, mid, right);
}
}
int main(void)
{
int arr[] = { 6, 3, 9, 1, 2, 7 };
int index = 0;
int arrSize = (sizeof(arr) / sizeof(int));
MergeSort(arr, 0, arrSize-1);
for (index = 0; index < arrSize; index++)
printf("%d ", arr[index]);
return 0;
}
합병 정렬의 성능은?
위 과정에서 < 3, 6, 9 >와 < 1, 2, 7 >을 한 덩어리로 합칠 때를 생각해봅시다.
- 1) 3과 1을 비교한다. 비교 연산 후에 1을 정렬된 배열로 이동한다.
- 2) 3과 2를 비교한다. 비교 연산 후에 2를 정렬된 배열로 이동한다.
- 3) 3과 7을 비교한다. 비교 연산 후에 3을 정렬된 배열로 이동한다.
- 4) 6과 7을 비교한다. 비교 연산 후에 6을 정렬된 배열로 이동한다.
- 5) 9와 7을 비교한다. 비교 연산 후에 7을 정렬된 배열로 이동한다.
- 마지막으로 남은 < 9 >를 정렬된 배열로 이동시키기 위한 if - else 문의 비교 연산
이렇게, 하나의 요소가 남을 때까지 비교 연산이 진행되는 경우는 최대의 연산 횟수인 n을 갖습니다. 합병 정렬은 정렬해야 할 요소 개수 n과 합병하는 과정의 횟수 k에 대해서 \(k=\log _{ 2 }{ n }\) 식이 성립됩니다. 즉, 빅오 표기법으로 합병 정렬의 비교 연산을 나타내면 \(O(n\log _{ 2 }{ n } )\) 입니다.
자세히 보면, 합병 과정에서 요소들이 이동되는 연산도 있습니다. 이동이 발생하는 이유는 ‘임시 배열에 요소들을 합치는 과정’에서 1회 발생하고 ‘임시 배열에 저장된 요소들 전부를 원래 위치로 이동하는 과정’에서 1회씩 발생합니다.
즉, 요소 이동으로 인한 연산 횟수는 최악, 평균, 최선의 경우와 상관없이 \(2n\log _{ 2 }{ n }\) 라고 볼 수 있지만 빅오 표기법에서 상수인 2는 무시할 수 있으므로 최종적인 빅오 표현은 \(O(n\log _{ 2 }{ n } )\) 라고 할 수 있습니다.
합병 정렬과 퀵 정렬
합병 정렬과 퀵 정렬은 비교하기 좋은 정렬 알고리즘입니다.
합병 정렬의 경우 작은 그룹을 정렬한 후 더 큰 그룹으로 합쳐나가는 Bottom-Up 방식입니다. 반면에 퀵 정렬은 큰 그룹에서부터 작은 그룹으로 연산이 진행되는 Top-Down 방식이지요.
또한, 퀵 정렬은 추가적인 저장 공간이 필요하지 않고 내부적인 교환만으로 정렬이 수행되지만 합병 정렬은 추가적인 저장 공간을 사용하여 정렬을 진행합니다.
성능 면으로는 합병 정렬의 경우 nlogn의 정렬 시간이 보장되며, 위치를 다시 배치하는 시간이 있기 때문에 거의 동일한 수행 시간을 갖지만 퀵 정렬은 최선의 경우 요소들의 개수인 n이며, 최악의 경우 n제곱까지 될 수 있습니다.
이러한 차이점이 있는 두 개의 정렬 방식은 모두 영역을 나누어 처리하는 분할 & 정복 알고리즘에 기반합니다.