이진 트리
이진 탐색 트리(Binary Search Tree)를 알아보기 전에 우선 이진 트리(Binary Tree)가 무엇인지 알아야한다. 정의는 비어있거나, 한 개의 루트와 다른 두 개의 다른 값을 가진 노드의 집합이다.
조금 더 풀어서 얘기하면, 최상의 루트 노드로부터 하위의 서브 트리 방향으로 점차 나아갈 때 각각 새롭게 루트가 되는 노드가 가지는 자식 노드의 개수가 2개 이하임을 말한다.
트리와 관련된 용어들
앞서 살펴본 이진 트리에도 여러가지 종류가 있습니다. 트리의 구성에 따라서 각각 다른 정의를 갖지요. 트리의 종류를 알아보기 전에 트리를 설명할 때 사용되는 용어에 대해서 먼저 알아봅시다.
- 방향 간선(Directed Edge)은 부모 노드에서 자식 노드로 가는 경로
- 루트 노드(Root Node)는 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
- 단말 노드(Leaf Node)는 자식이 없는 노드
- 각 노드의 깊이(Depth)는 루트 노드에서 자기 자신까지 가는 경로의 길이
- 차수(Degree)는 특정 노드가 가지는 자식 노드의 개수
- 트리의 높이(height)는 루트 노드에서 가장 깊이 있는 노드까지 가는 경로의 길이, 루트 노드만 있는 트리의 경우는 높이가 0이 된다.
- 형제 노드(Sibling Node)는 같은 부모를 가진 노드
트리의 종류
그럼 이제 이진 트리의 종류에 대해서 알아보자.
- 루트가 있는 트리(Rooted Binary Tree) : 모든 노드의 자식 노드가 최대 2개인 루트를 가진 트리
- 정 이진 트리(Full Binary Tree) : 단말 노드가 아닌 모든 노드가 2개의 자식 노드를 가진 트리
- 포화 이진 트리(Perfect Binary Tree) : 모든 단말 노드의 깊이가 같은 정 이진 트리(Full Binary Tree)
- 완전 이진 트리(Complete Binary Tree) : 끝부분을 제외하고 모든 노드가 채워진 이진 트리
그 밖에도 무한 완전 트리(Infinite Complete Binary Tree), 균형 이진 트리(Balanced Binary Tree) 그리고 변질 트리(Degenerate Tree) 등이 있다. 그림을 통해서 조금 더 자세히 살펴보자.
이진 트리
이진 트리(Binary Tree)의 정의는 모든 노드가 두 개 이하의 자식 노드를 가져야 한다. 그러니까 모든 노드의 차수(Degree)가 2 이하인 트리를 말한다. 그리고 이진 트리의 모든 서브 트리들은 모두 이진 트리다.
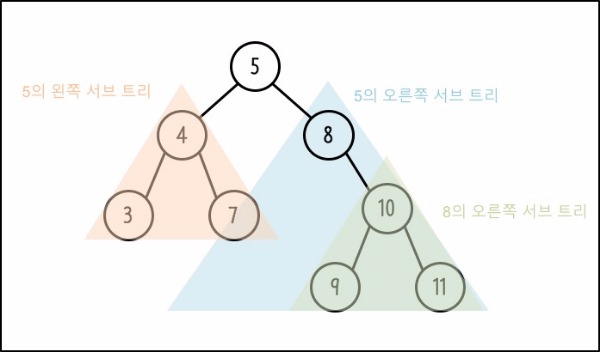
노드 5의 서브 트리는 루트가 4인 트리와 8인 트리가 있다. 또 노드 8은 루트가 10인 오른쪽 서브 트리를 가지고 있다.
앞서 살펴본 트리 관련 용어를 적용해보면 위 트리의 높이는 3이 된다. 루트의 깊이가 0일 때, 가장 깊이 있는 노드 9, 11 까지의 경로를 카운트하면 된다. 또한 노드 4의 차수(Degree)는 2이며 자식이 없는 단말 노드는 3, 7, 9, 11이 된다.
완전 이진 트리
다음으로 완전 이진 트리(Complete Binary Tree)를 살펴보자. 마지막 노드를 제외하고 모든 노드가 채워져 있는 트리를 말한다.
또한 마지막 레벨에서는 왼쪽부터 오른쪽으로 노드가 채워져있는 트리를 말한다.
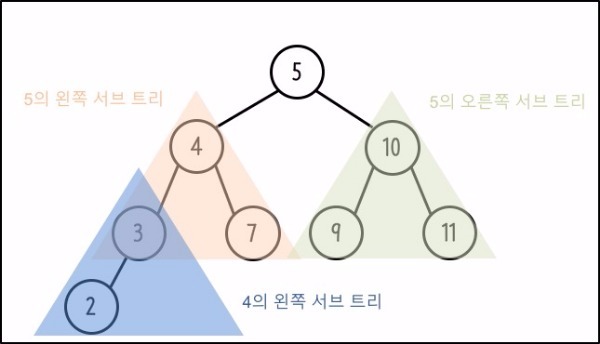
포화 이진 트리
마지막으로 포화 이진 트리(Perfect Binary Tree)를 살펴보자.
모든 노드가 가득 차 있어야 한다. 왼쪽이든 오른쪽이든 가득 차 있어야 한다.
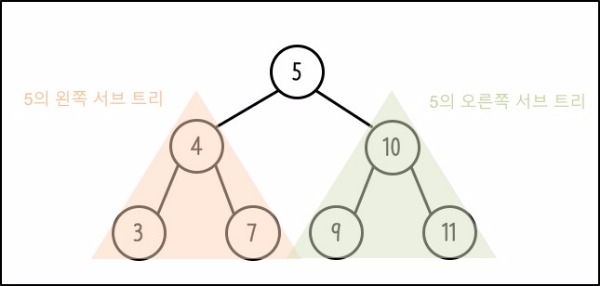
완전 이진 트리는 포화 이진 트리가 될 수 없지만, 포화 이진 트리는 완전 이진 트리라고 할 수 있다.
이진 탐색 트리
이진 탐색 트리는 이진 트리다. 하지만 조금 더 세부적인 정의를 갖고 있다.
- 1) 비어 있지 않다면 모든 노드(Node)는 서로 다른 값(Key)을 갖습니다.
- 2) 왼쪽 서브 트리에 포함된 값들은 만일 존재한다면, 루트의 값보다 항상 작은 값을 갖습니다.
- 3) 오른쪽 서브 트리에 포함된 값들은 만일 존재한다면, 루트의 값보다 항상 큰 값을 갖습니다.
- 4) 왼쪽과 오른쪽 서브 트리는 각각 루트 노드를 가진 또 하나의 이진 탐색 트리 구조여야 합니다.
이진 탐색 트리의 삽입과 삭제
이진 탐색 트리에 새로운 노드를 삽입하거나 특정 노드를 삭제하는 연산에 대해 살펴보자.
삽입 연산
삽입 연산은 새로운 노드가 위치할 곳을 탐색하는 과정이 필요합니다.
- 1-1) 루트 노드에 값이 없는 경우는 트리가 없는 경우이므로 루트에 넣는다.
- 1-2) 루트에 값이 있고 삽입되는 값이 루트보다 작으면 왼쪽으로 탐색시킨다.
- 1-3) 루트에 값이 있고 삽입되는 값이 루트보다 크면 오른쪽으로 탐색시킨다.
- 2) 해당 방향으로 탐색을 진행했을 때, 탐색 위치에 값이 없으면 해당 위치에 노드를 추가한다.
삭제 연산
삭제 연산은 삽입 연산에 비하여 조금 까다롭습니다. 삭제 대상 노드의 특성에 따라서 구분할 필요가 있습니다.
- 1) 우선 삭제할 노드의 값을 루트로부터 비교하는 탐색을 시작한다.
- 1-1) 삭제할 노드의 값이 루트보다 작으면 왼쪽으로 탐색하고 현재 포인터를 오른쪽 노드로 변경한다.
- 1-2) 삭제할 노드의 값이 루트보다 크면 왼쪽으로 탐색하고 현재 포인터를 왼쪽 노드로 변경한다.
- 2-1) 삭제하려는 노드가 단말 노드인 경우
- 2-1-1) 삭제 대상이 단말 노드이고 부모 노드의 왼쪽 자식 노드라면 부모 노드의 왼쪽 자식을 NULL로 만든다.
- 2-1-2) 삭제 대상이 단말 노드이고 부모 노드의 오른쪽 자식 노드라면 부모 노드의 오른쪽 자식을 NULL로 만든다.
- 2-2) 삭제하려는 노드가 한쪽 자식 노드만 가지는 경우
- 2-2-1) 오른쪽 자식 노드만 가진 경우, 삭제 대상 노드의 부모에게 자신의 오른쪽 자식 노드를 붙여준다.
- 2-2-2) 왼쪽 자식 노드만 가진 경우, 삭제 대상 노드의 부모에게 자신의 왼쪽 자식 노드를 붙여준다.
- 2-3) 삭제하려는 노드가 모든 자식 노드를 가지는 경우
- 2-3-1) 제되는 노드와 가장 비슷한 값을 선택하여야 한다. 그래야 다른 노드의 이동 없이 이진 탐색 트리가 유지된다.
- 2-4-1) 삭제 대상의 왼쪽 서브 트리에서 가장 큰 값을 선택한다.
- 2-4-2) 삭제 대상의 오른쪽 서브 트리에서 가장 작은 값을 선택한다.
이진 탐색 트리의 탐색
탐색은 이진 트리의 모든 노드를 방문하는 것을 말한다. 탐색 방법에는 대표적으로 전위(pre-order), 후위(post-order) 그리고 중위(in-order)가 있다.
- 전위 탐색 : 내 노드, 왼쪽 자식 노드, 오른쪽 자식 노드 순서로 방문합니다.
- 후위 탐색 : 왼쪽 자식 노드, 오른쪽 자식 노드, 내 노드 순서로 방문합니다.
- 중위 탐색 : 왼쪽 자식 노드, 내 노드, 오른쪽 자식노드 순서로 방문합니다.
정리하며
이번 글에서는 이진 탐색 트리(Binary Search Tree)에 대해서 알아보았다. 이어지는 글에서는 이진 탐색 트리를 구현하는 방법에 대해서 알아본다.