에라토스테네스의 체?

에라토스테네스의 체는 원리를 발견한 고대 그리스 수학자 에라토스테네스(Eratosthenes)의 이름에서 유래했습니다. 이름 그대로 자연수를 ‘체’ 라는 것을 이용하여 소수(Prime Number)만을 걸러내겠다는 것이지요.

이곳저곳 검색을 해보면 알 수 있듯이 소수를 판별하는 방법은 매우 많습니다. 기초적인 방법으로 하나하나씩 직접 판단하는 방법도 있고 제곱근으로 풀이하는 방법도 있습니다.

그래서 이번에는 조금 생소한 에라토스테네스의 체 라는 것을 이용해서 소수를 구해보고자 합니다.

어떤 방법일까?

우선, 소수(Prime Number)는 양의 양수를 두 개만 갖는 자연수를 소수라고 말합니다. 그러니까 2, 3, 5, 7, 11과 같은 수를 소수라고 합니다. 소수의 정의에 대해서도 알아보았으니 에라토스테네스의 체를 파헤쳐봅시다!

우선 1은 소수의 정의에 의해서 소수가 아니므로 제외합니다. 체를 친 것이지요. 그렇다면 이제 남은 숫자는 2 이상의 수가 됩니다.

남은 숫자들 중에서 가장 작은 숫자를 확인합니다. 숫자 2가 남지요. 앞에서 숫자 1은 체에 걸러졌으니까요! 앞서 언급한 소수의 정의에 의하면 숫자 2는 소수입니다.

그렇다면 2의 배수는 모두 체를 쳐서 걸러냅니다. 짝수는 모두 걸러내고 홀수만 남기는 것입니다. 이제 남은 숫자는 3 이상의 수가 됩니다.

또 다시 남은 숫자들 중에서 가장 작은 숫자를 확인합니다. 숫자 3이 가장 작습니다. 앞에서 숫자 1과 2는 걸러졌으니까요. 동일하게 소수의 정의에 의하면 숫자 3도 소수가 됩니다.

3의 배수도 모두 체를 쳐서 거릅시다. 그러니까 3, 6, 9, 12, 15, … 등등을 모두 걸러냅니다. 물론 숫자 2의 배수를 거르면서 6과 12 등은 이미 없습니다.

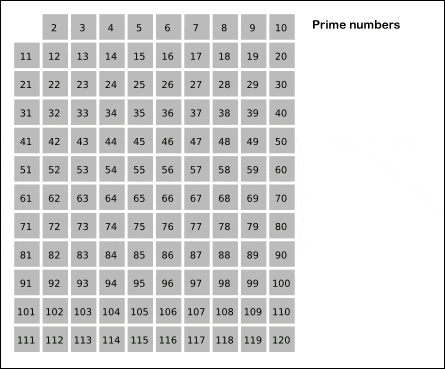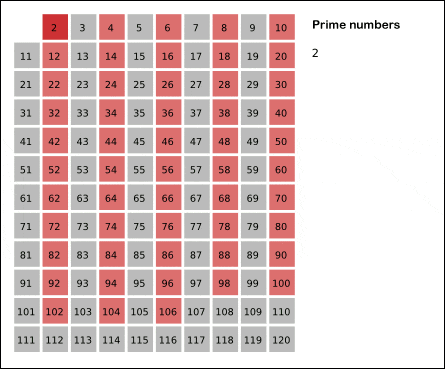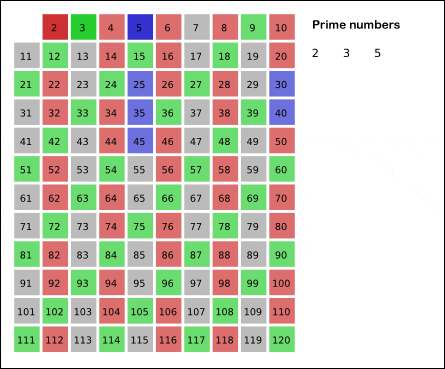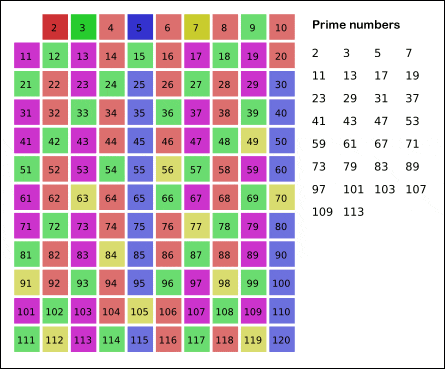
지겹지만 계속 해볼까요? 이제 남은 숫자들은 5, 7, 11, 13, 17, … 등이 되고 가장 작은 숫자는 5 입니다. 5의 배수를 체를 쳐서 걸러냅니다. 그러면 남은 숫자는 7, 11, 13, 17, … 등이 되고 가장 작은 숫자는 7 입니다. 7의 배수를 체를 쳐서 걸러냅니다. 이제 남은 숫자는 11, 13, 17, 19, … 등이 됩니다.

코드로 직접 구현해보자.

원리는 살펴보았으니 이제 코드로 구현해봅시다.

#include <stdio.h>
#include <stdlib.h>

#pragma warning(disable:4996)

int main(void)
{
    int maxNumber = 0;
    int *primeArray = NULL;
    int visited = 0;
    int check = 0;
    
    /* 최대 값을 입력한다. */
    printf("최대 값 입력 : ");
    scanf("%d", &maxNumber);
    
    /* 동적 할당한다. */
    primeArray = (int *)malloc(sizeof(int) * maxNumber);
    if (primeArray == NULL)
    {
        puts("메모리 할당 오류\n");
        exit(1);
    }
    
    /* 위에서 할당한 배열을 초기화한다. */
    for (visited = 2; visited <= maxNumber; visited++)
    {
        primeArray[visited] = visited;
    }
    
    /* 에라토스테네스의 체를 적용한다. */
    for (visited = 2; visited & visted <= maxNumber; visited++)
    {
        /* 이미 확인한 수의 배수는 검사하지 않는다. */
        if (primeArray[visited] == 0) continue;
        
        for(check = visited * visited; check <= maxNumber; check = check + visited)
        {
            /* 해당 배수들도 모두 체크한다. */
            primeArray[check] = 0;
        }
    }
    
    /* 결과를 출력한다. */
    for (visited = 2; visited <= maxNumber; visited++)
    {
        if (primeArray[visited]) printf("%d ", primeArray[visited]);
        if (visited % 10 ==0) printf("\n");
    }
}

위 코드의 실행 결과는 아래와 같습니다.

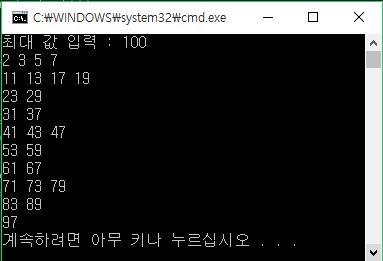
소수를 구하는 데 있어서 성능은?

에라토스테네스의 체를 적용한 코드의 시간 복잡도는 \(O(n\log { \log { n } ) }\) 이 됩니다.

소수를 구하는 방법이 참 많은 만큼 ‘소수(Prime Number)’ 라는 것 자체가 흥미로운 부분이 많습니다. 원거리 통신, 국가 안보 등에 깊숙하게 관련되어 있고 더 큰 소수를 찾기 위한 노력이 계속되고 있다고 하네요.

네이버 백과사전을 인용해보면, 현재까지 발견된 소수 중 가장 큰 것을 적기 위해서는 무려 신문 12개 면이 필요한 37만 8천 6백 32자리의 숫자라고 합니다.