퀵 정렬이란 무엇일까?

퀵 정렬에 사용되는 용어부터 살펴봅시다.

용어	설명
Pivot	정렬의 중심을 말합니다. 읽을 때는 피벗(Pivot)이라고 읽습니다.
Low	Pivot을 제외한 가장 왼쪽에 위치한 지점을 가리킵니다.
High	Pivot을 제외한 가장 오른쪽에 위치한 지점을 가리킵니다.
Left	정렬한 요소들의 가장 왼쪽 지점을 가리킵니다
Right	정렬할 요소들의 가장 오른쪽 지점을 가리킵니다.

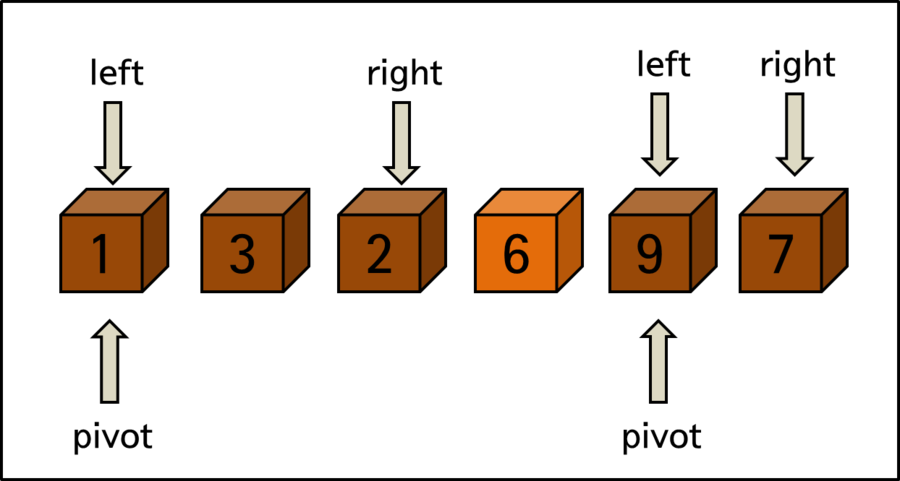
아래 예시 그림을 통해서 조금 더 자세히 살펴봅시다. 여기서 pivot은 가장 왼쪽에 위치한 < 요소 6 > 입니다.

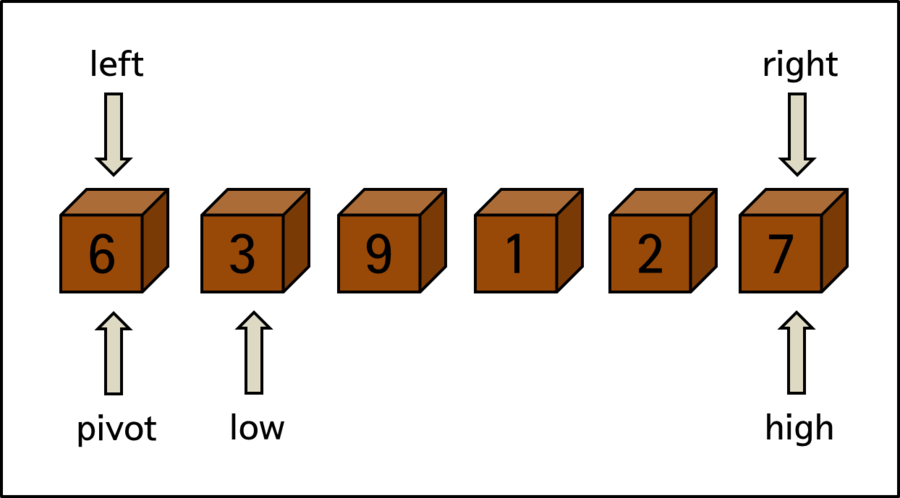
퀵 정렬 용어 설명

low는 < 요소 3 > 이며 오른쪽 방향으로 움직이면서 정렬을 진행합니다. 반대로 high는 < 요소 7 > 이며 왼쪽 방향으로 움직이면서 정렬을 진행합니다. 물론 low와 high는 번갈아가면서 한 칸씩 움직이는 것이 아니라 별개로 진행됩니다.

퀵 정렬 진행

진행 규칙은 간단합니다. high는 pivot 보다 작은 값을 찾고 반대로 low는 pivot 보다 큰 값을 찾습니다. 조건에 맞는 값을 찾는 경우 high와 low가 찾은 값을 서로 교환하는 것이지요.

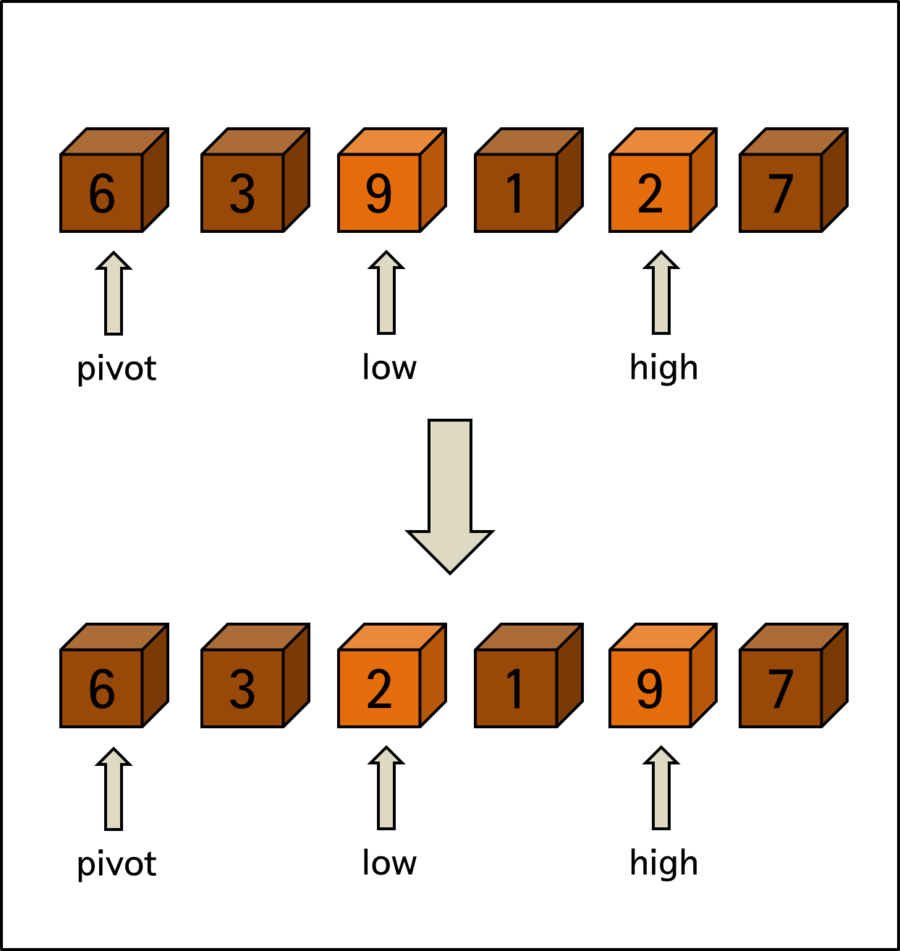
퀵 정렬 Step 1

< 교환 1회 진행 > 후의 모습입니다. high가 찾은 < 요소 2 >와 low가 찾은 < 요소 9 >가 교환되었습니다. high와 low가 서로 교환된 후에도 high는 왼쪽 방향으로 pivot 보다 더 큰 값을 찾아 이동하고 low는 오른쪽 방향으로 pivot 보다 더 작은 값을 찾아 움직입니다.

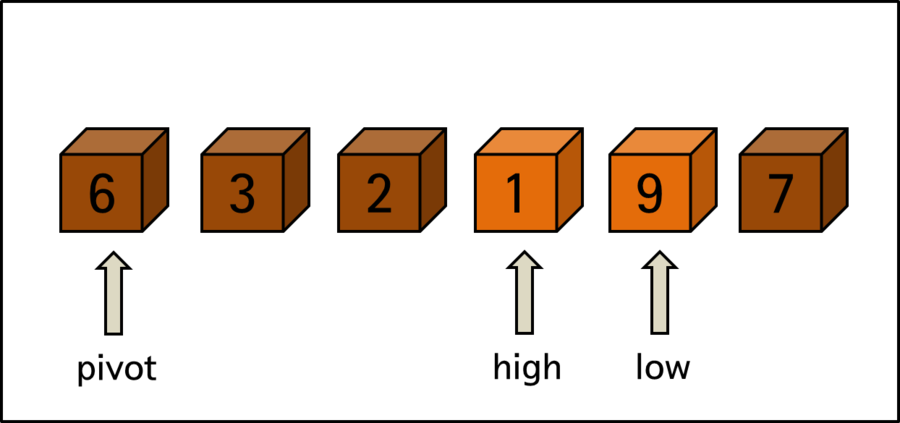
퀵 정렬 Step 2

high는 pivot인 < 요소 6 >보다 작은 < 요소 1 >을 발견했고, low는 pivot보다 큰 < 요소 9 >를 찾았습니다. 하지만, 지금처럼 high와 low가 서로 교차되는 경우에는 서로 값을 교환하지 않습니다. 그 이유는 high와 low의 이동과 교환이 완료가 되었음을 뜻하기 때문이지요.

"이런 상황에서는 pivot과 high가 가리키는 값을 바꾸게 됩니다."

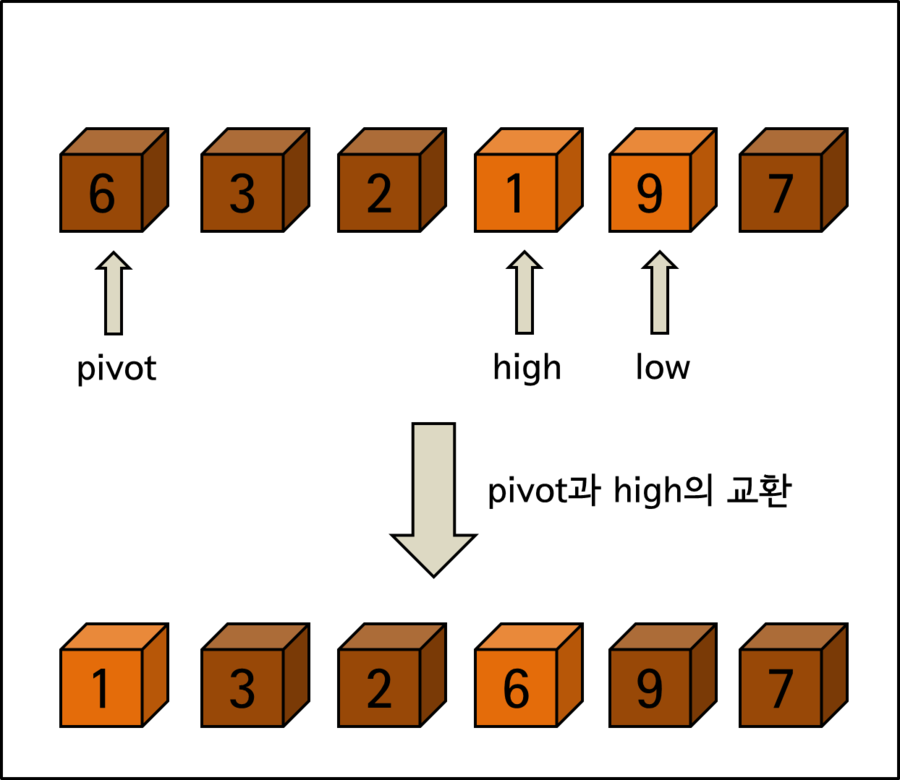
퀵 정렬 Step 3

이동한 pivot 값의 위치를 보면 앞에서 네 번째에 위치해있습니다. 정렬 대상이 6개의 요소밖에 되지 않아 눈치채신 분들도 계시겠지만 방금 교환으로 인하여 < 요소 6 >은 자신의 정렬 위치를 찾게 되었습니다.

이후에는 자신의 정렬 위치를 찾은 < 요소 6 >을 기준으로 왼쪽과 오른쪽 영역으로 나뉘어 위 과정을 다시 진행하게 됩니다.

퀵 정렬 Step 4

퀵 정렬 구현

위의 퀵 정렬 과정을 소스 코드로 살펴봅시다.

#include <stdio.h>
#include <stdlib.h>

void Swap(int arr[], int firstIndex, int secondIndex)
{
    int temp = arr[firstIndex];
    arr[firstIndex] = arr[secondIndex];
    arr[secondIndex] = temp;
}

int Partition(int arr[], int left, int right)
{
    // pivot의 위치는 가장 왼쪽 요소로 정한다.
    int pivot = arr[left];
    int low = left + 1;
    int high = right;

    // low와 high가 교차되지 않을 때까지
    while (low <= high)
    {
        // low는 피벗보다 큰 값을 찾는다.
        while (pivot >= arr[low] && low <= right)
            low++;

        // high는 피벗보다 작은 값을 찾는다.
        while (pivot <= arr[high] && high >= (left+1))
            high--;
 
        // low와 high가 교차하지 않았다면 두 값을 교환한다.
        if (low <= high) Swap(arr, low, high);
    }
    // 피벗과 high를 교환한다.
    Swap(arr, left, high);
    return high;
}

void QuickSort(int arr[], int left, int right)
{
    if (left <= right)
    {
        // 분할한다.
        int pivot = Partition(arr, left, right);

        // 왼쪽에 위치한 요소들을 정렬한다.
        QuickSort(arr, left, pivot - 1);
 
        // 오른쪽에 위치한 요소들을 정렬한다.
        QuickSort(arr, pivot + 1, right);
    }
}

int main(void)
{
    int arr[] = { 6, 3, 9, 1, 2, 7 };
    int index = 0;
    int arrSize = (sizeof(arr) / sizeof(int));
 
    QuickSort(arr, 0, arrSize - 1);

    for (index = 0; index < arrSize; index++)
        printf("%d ", arr[index]);
 
    return 0;
}

low의 값을 증가시키고 high의 값을 감소시키는 반복문의 조건 하나씩 살펴봅시다. 먼저 low의 증가 조건입니다.

/* pivot 보다 더 큰 값을 찾아야 하는 조건 */
1) pivot >= arr[low]

/* low의 값이 right의 값보다 더 커지게 되는 경우는 배열의 최대 인덱스 범위를 넘어간 것으로 판단 */
2) low <= right

다음으로 high의 감소 조건입니다.

/* high는 pivot 보다 더 작은 값을 찾아야 하는 조건 */
1) pivot >= arr[low]

/* high의 값이 (left + 1)보다 작아지는 경우는 pivot을 가리키거나 배열의 최소 인덱스 넘어 가는 것으로 판단 */
2) high >= (left + 1)

pivot의 위치에 대해서

이번 포스팅에서 진행한 것처럼 가장 왼쪽에 있는 요소를 pivot으로 지정하는 경우 불균등하게 나뉠 수 있는 이슈가 있습니다. 예제와 다르게 pivot이 중간에 위치하면 정렬 요소들이 균등하게 나누어집니다. 이러한 이유로 pivot의 위치를 중간에 있는 요소로 지정하면 가장 좋은 성능을 보입니다.

즉, 전체의 요소를 탐색해서 중간값을 찾는 작업은 시간이 걸리기 때문에 pivot은 좌측 끝, 중앙, 우측 끝 중 중간값을 이용해서 정합니다.

퀵 정렬의 성능은?

pivot이 자신의 자리를 찾아가는 과정에서 발생하는 비교 연산은 요소들의 개수인 n번 만큼 발생합니다. 물론 pivot인 자기 자신으로 인해 n보다 하나 적은 횟수의 비교 연산이 진행되지만, 이는 무시됩니다.

분할이 몇 단계로 이루어지는 지도 살펴봐야 합니다. 요소의 개수가 31개라고 가정해봅시다. 가장 이상적으로 pivot의 위치가 중간으로 결정된다고 가정한다면 첫 번째 분할 과정에서 전체 요소들은 15개씩 둘로 나뉩니다. 그리고 다음 번 분할에서 각각 7개씩 나뉘어 총 4개의 영역으로 구분됩니다. 이 영역들은 또 다시 3개씩의 요소들로 나뉘어 3개씩의 요소들로 나뉘어 총 8개의 영역으로 구분되며 최종적으로는 1개씩 나뉘어 총 16개의 영역으로 구분됩니다.

분할하는 횟수를 k라고 가정할 때 요소들의 개수 n과 k는 \(k=\log _{ 2 }{ n }\)으로 표현할 수 있습니다. 즉, 퀵 정렬의 비교 횟수는 \(n\log _{ 2 }{ n }\) 이며 빅-오 표기법으로 표현하면 \(o(n\log _{ 2 }{ n } )\) 입니다.

하지만 요소들이 이미 정렬된 상태에서 pivot이 가장 작은 값(예제처럼 pivot을 지정)이라면 \(k=n\) 이 됩니다. 즉, 최악의 경우는 \(o({ n }^{ 2 })\) 가 성립됩니다.