Levenshtein Distance?

It’s an algorithm devised by Russian scientist Vladimir Levenshtein. It’s also called Edit Distance. Levenshtein Distance is an algorithm that can find how similar two strings A and B are when given. That is, it can calculate how many operations need to be performed for string A to become the same as string B.

Understanding Through Simple Examples

Understanding Levenshtein distance through simple examples. Assume string A is ‘delegate’ meaning ‘representative’ and string B is ‘delete’ meaning ‘delete’.

If the 5th character g and 6th character a in string A are deleted, string B becomes identical. That is, the operation count here becomes 2.

Consider another example using different strings. Assume string A is ‘process’ meaning ‘process’ and string B is ‘professor’ meaning ‘professor’.

First, replace character c at position 4 in string A with character f. The result becomes profess. Next, insert character o at the last position. The result at this time becomes professo. Finally, insert character r at the very last position again. Finally, ‘professor’ identical to string B is completed.

Here, since we performed 1 replacement operation and 2 insertion operations, the total operation count is 3.

Where Is It Used?

Like measuring similarity between strings we saw as examples, it can basically be used to find similarity between two data. Especially, it can be used for program plagiarism detection, spelling error checking, etc. Looking up fields where it can be used, it’s said to be used not only in natural language translation but also in gene similarity determination in genetics and medical engineering.

Pseudo Code

Examining Levenshtein distance (or edit distance) in pseudo code:

int LevenshteinDistance(char s[1..m], char t[1..m])
{
    declare int d[0..m, 0..n]
    clear all elements in d // set each element to zero
    
    for i from 1 to m
        d[i, 0] := i
    
    for j from 1 to n
        d[0, j] := j
        
    for j from 1 to n
    {
        for i from 1 to m
        {
            if s[i] = t[j] then d[i, j] := d[i-1, j-1]
            else d[i, j] := minimum(d[i-1, j]+1, d[i, j-1]+1, d[i-1, j-1]+1)
        }
    }
    return d[m, n]
}

The part to carefully examine is line 17’s code. It’s the part where operation count is added when values are not the same when searching strings A and B at the same index. You can examine the process as a matrix as shown below.

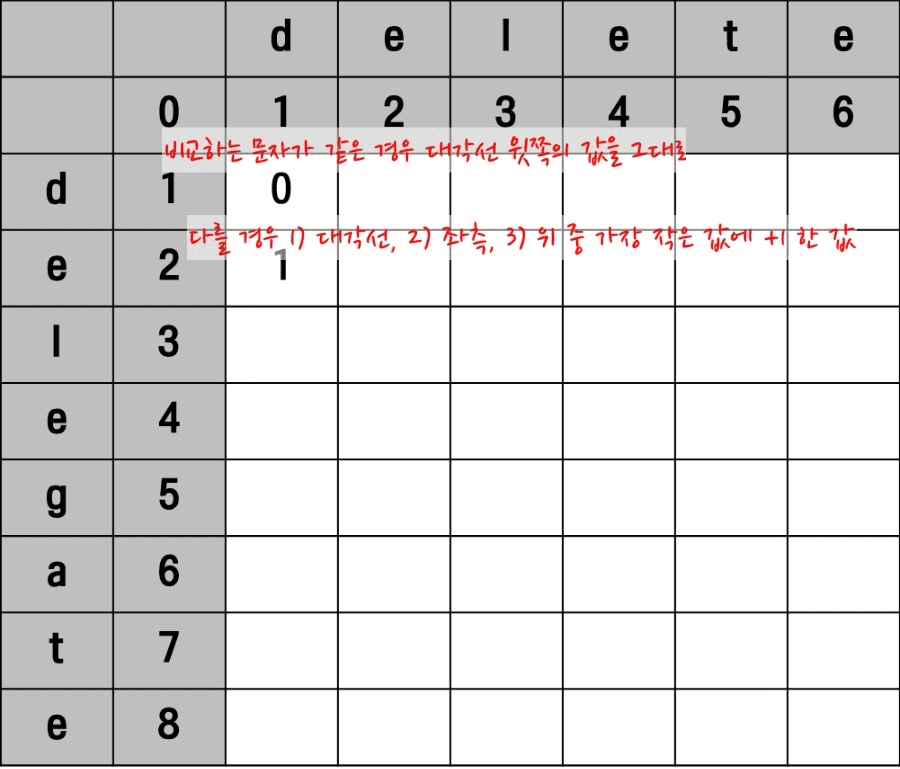
The first character of string A’s delegate and string B’s delete are both ‘d’, so they’re the same. Therefore, like line 16’s code of the algorithm expressed in pseudo code above, it takes the value diagonally above as is.

Next, string A’s second character e and string B’s first character d are different characters. In such cases, like line 17’s code, it takes the value of the smallest among diagonally above, left, and directly above plus 1.

If we continue this process, we can confirm the final matrix appearance as shown below.

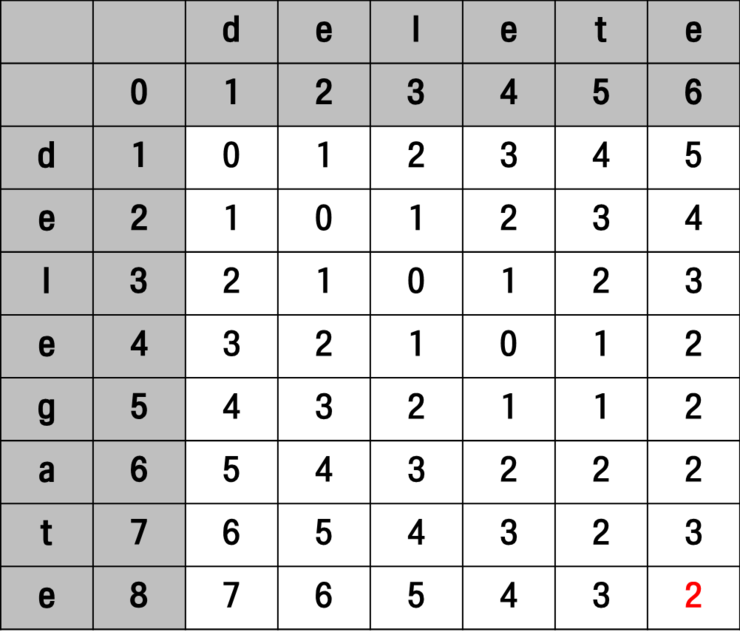
The number 2 at the bottom right means the number of operations for string (delegate) A to become the same as string (delete) B.

Implementing in Java Code

Finally, implementing the edit distance (or Levenshtein) algorithm in Java code:

public class MadLife {

    public int getMinimum(int val1, int val2, int val3) {
        int minNumber = val1;
        if(minNumber > val2) minNumber = val2;
        if(minNumber > val3) minNumber = val3;
        return minNumber;
    }

    public int levenshteinDistance(char[] s, char[] t) {
        int m = s.length;
        int n = t.length;

        int[][] d = new int[m + 1][n + 1];

        for (int i = 1; i < m; i++) {
            d[i][0] = i;
        }

        for (int j = 1; j < n; j++) {
            d[0][j] = j;
        }

        for (int j = 1; j < n; j++) {
            for (int i = 1; i < m; i++) {
                if (s[i] == t[j]) {
                    d[i][j] = d[i - 1][j - 1];
                } else {
                    d[i][j] = getMinimum(d[i - 1][j], d[i][j - 1], d[i - 1][j - 1]) + 1;
                }
            }
        }
        return d[m - 1][n - 1];
    }

    public void runAlgorithm() {
        char[] stringA = "delegate".toCharArray();
        char[] stringB = "delete".toCharArray();

        int result = levenshteinDistance(stringA, stringB);
        System.out.println(result);
    }

    public static void main(String[] args) {
        new MadLife().runAlgorithm();
    }
}