리벤슈테인 거리?

러시아 과학자 블라디미르 리벤슈테인(Vladimir Levenshtein)가 고안한 알고리즘입니다. 편집 거리(Edit Distance) 라는 이름으로도 불립니다. Levenshtein Distance는 두 개의 문자열 A, B가 주어졌을 때 두 문자열이 얼마나 유사한 지를 알아낼 수 있는 알고리즘입니다. 그러니까, 문자열 A가 문자열 B와 같아지기 위해서는 몇 번의 연산을 진행해야 하는 지 계산할 수 있습니다.

간단한 예시로 이해해보자.

간단한 예시를 통해 리벤슈테인 거리를 이해해봅시다. 문자열 A가 ‘대표자’ 라는 뜻을 가진 ‘delegate’ 라고 가정하고 문자열 B는 ‘삭제’ 라는 뜻을 가진 ‘delete’ 라고 가정합니다.

문자열 A에서 5번 째 문자 g와 6번 째의 문자 a가 삭제되면 문자열 B가 동일해집니다. 즉, 여기서의 연산 횟수는 2가 되는 것이지요.

다른 문자열을 이용해서 또 다른 예를 들어봅시다. 문자열 A가 ‘과정’ 을 뜻하는 ‘process’ 라고 가정하고 문자열 B가 ‘교수’ 를 뜻하는 ‘professor’ 라고 가정해봅시다.

먼저, 문자열 A에서 4번 째에 위치한 문자 c를 문자 f로 대체합니다. 그 결과는 profess가 됩니다. 그 다음으로 마지막에 위치에 문자 o를 삽입합니다. 이 때의 결과는 professo가 됩니다. 마지막으로 또 다시 가장 마지막 위치에 문자 r을 삽입합니다. 최종적으로 문자열 B와 동일한 ‘professor’가 완성됩니다.

여기서는 1번의 대체 연산과 2번의 삽입 연산을 진행했으므로 총 연산 횟수는 3이 됩니다.

어디에 사용할까요?

예시로 살펴본 문자열 간의 유사도 측정처럼 기본적으로는 두 데이터 사이의 유사도를 알아내기 위해 사용할 수 있습니다. 특히 프로그램의 표절 여부, 철자 오류 검사 등에 사용할 수 있지요. 사용할 수 있는 분야들을 찾아보니 자연어 번역뿐만 아니라 유전 및 의료 공학에서의 유전자 유사도 판별에도 사용한다고 합니다.

의사 코드(Pseudo code)

의사 코드로 리벤슈테인 거리(또는 편집거리)를 살펴봅시다.

int LevenshteinDistance(char s[1..m], char t[1..m])
{
    declare int d[0..m, 0..n]
    clear all emenets in d // set each element to zero
    
    for i from 1 to m
        d[i, 0] := i
    
    for j from 1 to n
        d[0, j] := j
        
    for j from 1 to n
    {
        for i from 1 to m
        {
            if s[i] = t[j] then d[i, j] := d[i-1, j-1]
            else d[i, j] := minimum(d[i-1, j]+1, d[i, j-1]+1, d[i-1, j-1]+1)
        }
    }
    return d[m, n]
}

주의깊게 살펴야 하는 부분은 17번 라인의 코드입니다. 동일한 인덱스에서 문자열 A와 B를 탐색했을 때 값이 서로 같지 않은 경우에 연산 횟수가 더해지는 부분입니다. 아래와 같이 매트릭스(행렬)로 진행 과정을 살펴볼 수 있습니다.

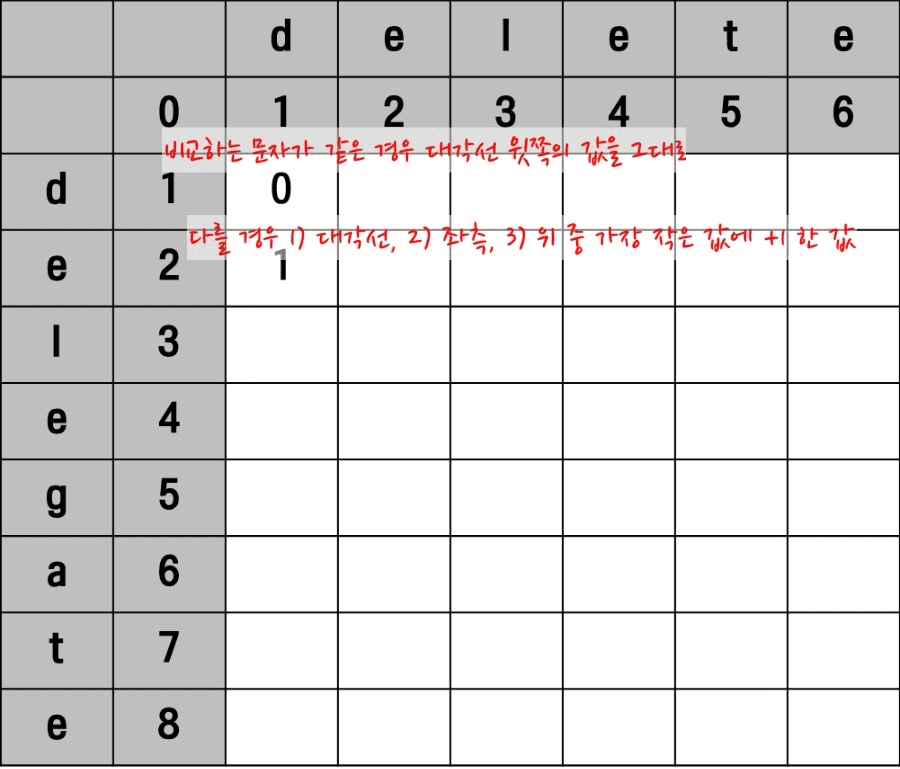
문자열 A의 delegate와 문자열 B의 delete의 첫 번째 문자는 둘 다 ‘d’이므로 같습니다. 따라서 위의 의사 코드(pseudo code)로 표현한 알고리즘의 16번 라인의 코드처럼 대각선으로 위에 있는 값을 그대로 갖습니다.

다음으로 비교되는 문자열 A의 두 번째 문자 e와 문자열 B의 첫 번째 d는 서로 다른 문자입니다. 이러한 경우는 17번 라인의 코드처럼 대각선 위, 좌측, 바로 위 중 가장 작은 값에 1을 더한 값을 갖습니다.

이러한 과정을 계속 진행해보면 아래와 같이 최종적인 매트릭스의 모습을 확인할 수 있습니다.

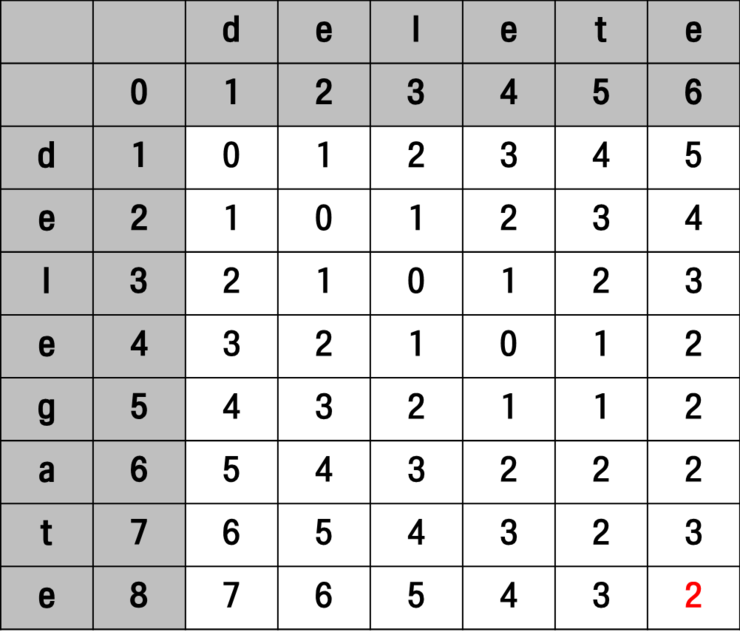
우측 가장 하단에 있는 숫자 2가 뜻하는 것은 문자열(delegate) A가 문자열(delete) B와 서로 같아지기 위한 연산의 횟수가 됩니다.

자바 코드로 구현하기

마지막으로 편집 거리(또는 리벤슈테인) 알고리즘을 Java 코드로 구현해봅시다.

public class MadLife {

    public int getMinimum(int val1, int val2, int val3) {
        int minNumber = val1;
        if(minNumber > val2) minNumber = val2;
        if(minNumber > val3) minNumber = val3;
        return minNumber;
    }

    public int levenshteinDistance(char[] s, char[] t) {
        int m = s.length;
        int n = t.length;

        int[][] d = new int[m + 1][n + 1];

        for (int i = 1; i < m; i++) {
            d[i][0] = i;
        }

        for (int j = 1; j < n; j++) {
            d[0][j] = j;
        }

        for (int j = 1; j < n; j++) {
            for (int i = 1; i < m; i++) {
                if (s[i] == t[j]) {
                    d[i][j] = d[i - 1][j - 1];
                } else {
                    d[i][j] = getMinimum(d[i - 1][j], d[i][j - 1], d[i - 1][j - 1]) + 1;
                }
            }
        }
        return d[m - 1][n - 1];
    }

    public void runAlgorithm() {
        char[] stringA = "delegate".toCharArray();
        char[] stringB = "delete".toCharArray();

        int result = levenshteinDistance(stringA, stringB);
        System.out.println(result);
    }

    public static void main(String[] args) {
        new MadLife().runAlgorithm();
    }
}