선택 정렬이란 무엇일까?

선택 정렬이란 정렬이 되지 않은 전체 데이터 중에서 해당 위치에 맞는 데이터를 선택하여 위치를 교환하는 제자리 정렬 알고리즘입니다. 아래와 같은 절차로 진행됩니다.

1) 주어진 데이터 리스트 중에서 제일 작은 값을 갖는 데이터를 찾는다.
2) 찾은 데이터를 가장 처음에 위치한 데이터의 위치와 교체한다.
3) 가장 처음 위치를 제외한 나머지 데이터도 같은 방법으로 교체한다.

이를 의사 코드(Pseudo Code)로 나타내면 아래와 같습니다.

For i -> 0 to n:
    a[i] to a[n-1] 까지 비교한 데이터 중 가장 작은 데이터가 a[j]에 있다면,
    a[i] and a[j] swapping 

선택 정렬 진행

그림으로 선택 정렬의 진행 과정을 자세히 살펴봅시다. 시작 상태에 대한 포함 여부(초기 상태로 주느냐 안 주느냐)에 따라서 회전 횟수(PASS)를 세는 방식이 다를 수 있습니다.

"여기서는 위치를 변경하는 경우만 N 회전(PASS)로 계산합니다."

선택 정렬 Step1

선택 정렬 Step2

선택 정렬 Step3

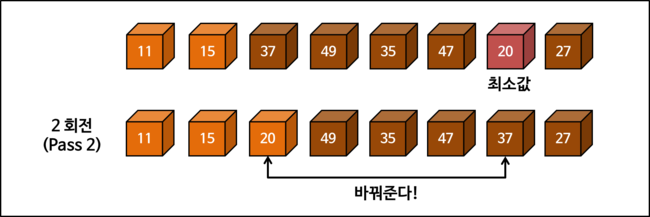
선택 정렬 Step4

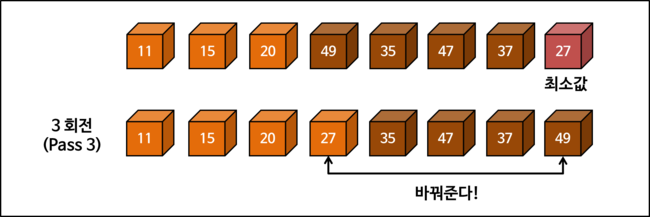
선택 정렬 Step5

선택 정렬 Step6

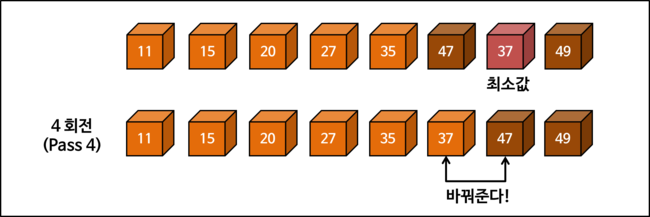
선택 정렬 Step7

선택 정렬 Step8

선택 정렬 Step9

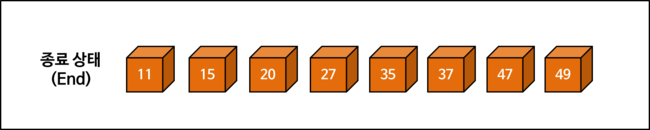
선택 정렬 Step10

선택 정렬 구현

위 과정을 소스 코드를 통해 살펴봅시다.

void selectionSort(int *list, const int n)
{
    int i, j, indexMin, temp;

    for (i = 0; i < n - 1; i++)
    {
        indexMin = i;
        for (j = i + 1; j < n; j++)
        {
            if (list[j] < list[indexMin])
            {
                indexMin = j;
            }
        }
        temp = list[indexMin];
        list[indexMin] = list[i];
        list[i] = temp;
    }
}

선택 정렬의 성능

복잡도를 살펴볼까요? 최선(min), 평균(ave), 최악(max)의 경우일 때 정렬을 위한 비교 횟수를 C라고 하면 아래와 같이 나타낼 수 있습니다.

\[{ C }_{ min }{ =C }_{ ave }={ C }_{ max }=\sum _{ i=1 }^{ N-1 }{ N-i } =\frac { N(N-1) }{ 2 } =O({ n }^{ 2 })\]

여기서 N은 데이터의 개수를 나타냅니다.