Real numbers in Java
Java provides float and double for real numbers.
Like integer types int and long, they use 4 and 8 bytes.
But based on floating-point representation (splitting into mantissa and exponent), they represent a wider range than integers.
In Java, double is the default for real-number operations.
Decimal representation
Computers use binary due to hardware signal handling. A signal means 1, and no signal means 0.
So real numbers are also represented in binary, which is more complex than integers. There are two major approaches: Fixed-Point Number Representation and Floating-Point Number Representation.
Fixed-point
Fixed-point assigns fixed digits before/after the decimal point. It represents decimal numbers with fixed precision.
The first bit is the sign bit. 0 means positive, 1 means negative. The remaining bits are split into integer part and fractional part around the decimal point.
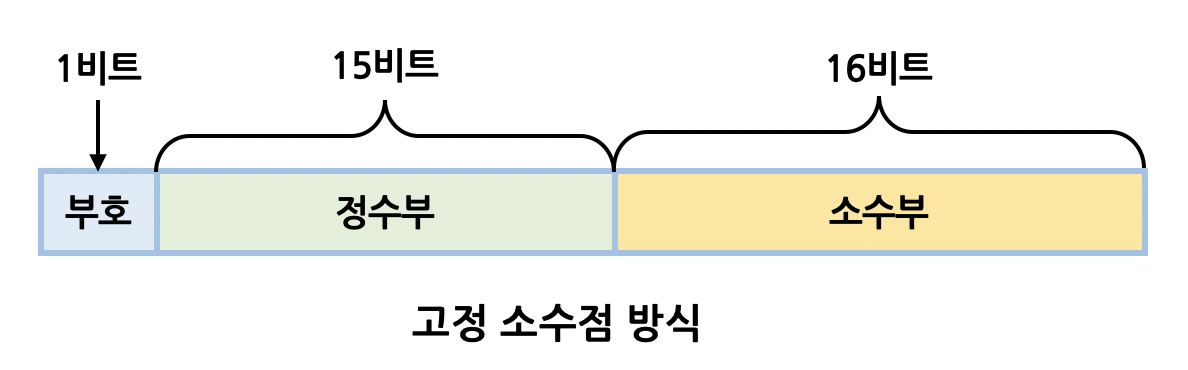
As shown, fixed-point keeps decimal position fixed.
For example, 7.75 is 111.11 in binary.
In fixed-point (assuming 16 bits for convenience), it is represented as below.
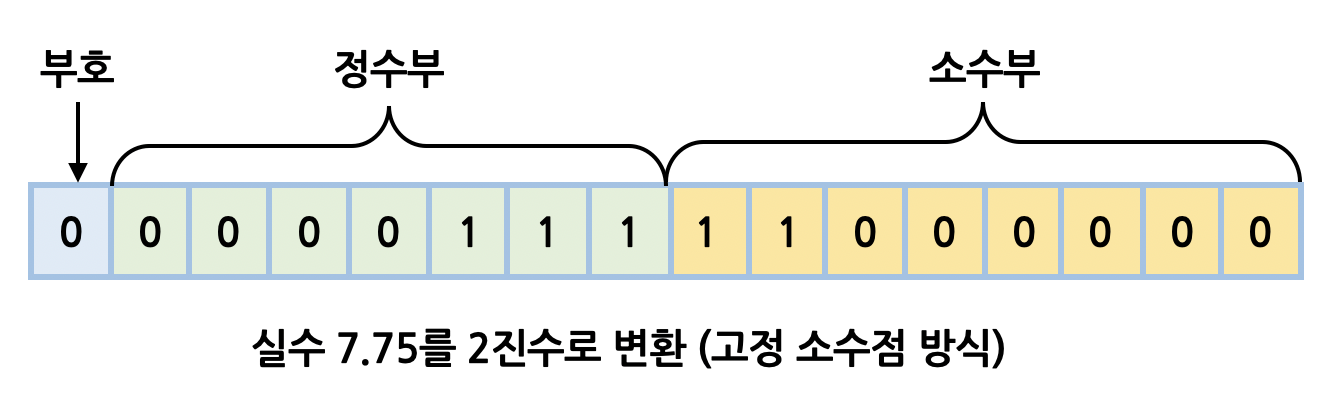
Because fixed-point has limited digits, representable range and precision are constrained, so it is not widely used.
Floating-point
Most floating-point systems follow IEEE 754, and this post follows that standard.
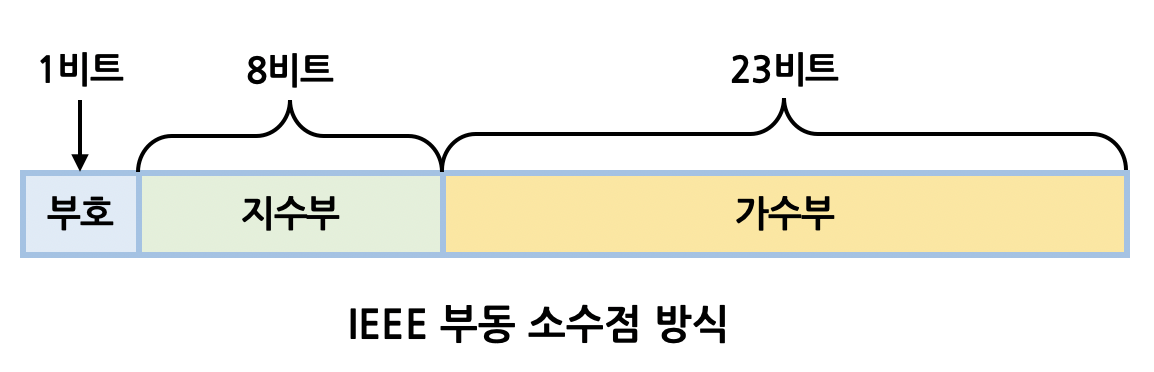
Floating-point represents real numbers differently from fixed-point. It splits values into sign, mantissa, and exponent.
The base expression is \({ (-1) }^{ S }\) x \({ M }\) x \({ 2 }^{ E }\), where:
- S: Sign, 1 bit. 0 positive, 1 negative.
- M: Mantissa, 23 bits, represented as positive integer.
- E: Exponent, 8 bits, represents decimal point position.
For example, real number -12.34 in floating-point is represented as below.
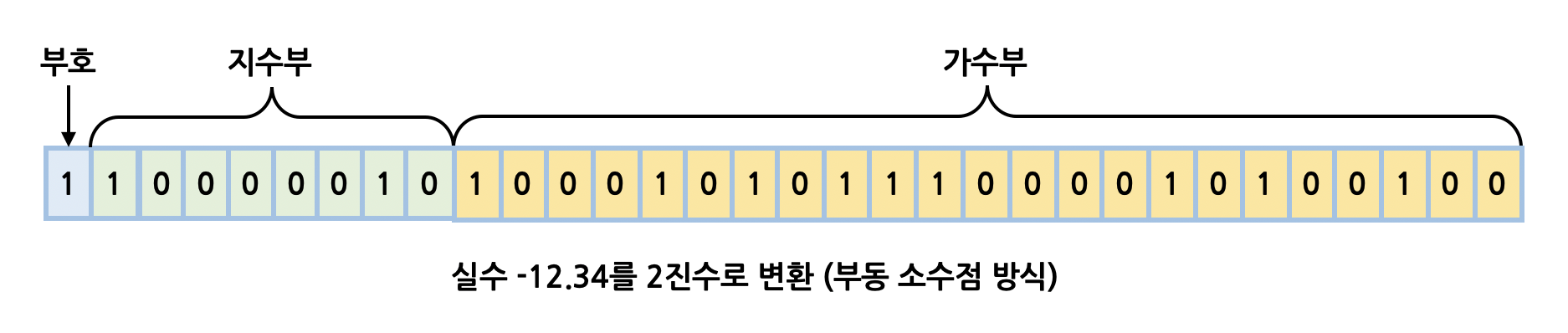
Compared with fixed-point, floating-point supports much wider range and higher precision, so most modern systems use floating-point for real numbers.
Floating-point error
As described above, floating-point has wider range than fixed-point, but precision issues still exist. So even with floating-point, errors can appear. Real-number representation in computers should be understood as approximation.
Run the example below:
double value1 = 12.23;
double value2 = 34.45;
// 46.68 ???
value1 + value2;
You might expect 46.68, but actual output is 46.68000000000001. Real-number operations use approximations instead of exact decimal representation, so error can occur.
This difference is small, but in financial systems it can have significant impact. How can we solve it?
Solution: BigDecimal
To address floating-point error, Java provides BigDecimal.
For decimal arithmetic, BigDecimal is essential.
Declaration
BigDecimal is in java.math.
The typical approach is constructor with a string argument, and static factory methods are also available.
Important: do not pass double directly to constructor.
// constructor + string initialization
BigDecimal value1 = new BigDecimal("12.23");
// initialize from double
// internally uses constructor + string
BigDecimal value2 = BigDecimal.valueOf(34.45);
// do not use like below
// 12.230000000000000426325641456060111522674560546875
BigDecimal dontDoThis = new BigDecimal(12.23);
Arithmetic operations
Add
Use add.
BigDecimal.ONE is a global constant from BigDecimal.
ZERO and TEN are also provided.
BigDecimal value = new BigDecimal("12.23");
// 13.23
value.add(BigDecimal.ONE);
Subtract
Use subtract.
BigDecimal value = new BigDecimal("12.23");
// 2.23
value.subtract(BigDecimal.TEN);
Multiply
Use multiply.
BigDecimal value = new BigDecimal("1");
// 10
value.multiply(BigDecimal.TEN);
Divide
Use divide.
But for non-terminating decimals, it throws ArithmeticException.
BigDecimal value1 = new BigDecimal("11");
BigDecimal value2 = BigDecimal.valueOf(3);
// Exception in thread "main" java.lang.ArithmeticException:
// Non-terminating decimal expansion; no exact representable decimal result.
value1.divide(value2);
Even with BigDecimal, some division results are not exactly representable.
So when using divide, you must specify scale and rounding mode.
In the example below, second parameter is scale and third is rounding mode. So it rounds at the 3rd decimal place and keeps 2 digits.
BigDecimal.ROUND_HALF_UP-style constants were deprecated in Java 9.
BigDecimal value1 = new BigDecimal("11");
BigDecimal value2 = BigDecimal.valueOf(3);
// 3.67
value1.divide(value2, 2, RoundingMode.HALF_UP);
Other methods
Remainder
Use remainder.
BigDecimal value = new BigDecimal("10");
// 2
value.remainder(BigDecimal.valueOf(4));
Compare values
Use compareTo.
Returns -1 if smaller than parameter, 1 if larger, 0 if equal.
BigDecimal value = new BigDecimal("10");
// 0
value.compareTo(BigDecimal.TEN);
// 1
value.compareTo(BigDecimal.ONE);
// -1
BigDecimal.ONE.compareTo(value);
Max/Min
Use max and min.
BigDecimal value = BigDecimal.valueOf(10);
// 10
value.max(BigDecimal.ONE);
// 1
value.min(BigDecimal.ONE);
Decimal rounding modes
Java provides multiple rounding modes via BigDecimal.
Examples:
// keep 1 decimal place, round at second decimal
// 12.4
BigDecimal.valueOf(12.35).setScale(1, RoundingMode.HALF_UP);
// remove all fractional part, round up
// 13
BigDecimal.valueOf(12.34).setScale(0, RoundingMode.CEILING);
// for negative numbers, remove below specific digit
// -12.3
BigDecimal.valueOf(-12.34).setScale(1, RoundingMode.CEILING);
// truncate below specific digit
// 12.3
new BigDecimal("12.37").setScale(1, RoundingMode.FLOOR);
The table below summarizes RoundingMode in BigDecimal.
It applies rounding at the first decimal place (setScale(0, RoundingMode)).
| Input | UP | DOWN | CEILING | FLOOR | HALF_UP | HALF_DOWN | HALF_EVEN |
|---|---|---|---|---|---|---|---|
| 5.5 | 6 | 5 | 6 | 5 | 6 | 5 | 6 |
| 2.5 | 3 | 2 | 3 | 2 | 3 | 2 | 2 |
| 1.6 | 2 | 1 | 2 | 1 | 2 | 2 | 2 |
| 1.1 | 2 | 1 | 2 | 1 | 1 | 1 | 1 |
| 1.0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| -1.0 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| -1.1 | -2 | -1 | -1 | -2 | -1 | -1 | -1 |
| -1.6 | -2 | -1 | -1 | -2 | -2 | -2 | -2 |
| -2.5 | -3 | -2 | -2 | -3 | -3 | -2 | -2 |
| -5.5 | -6 | -5 | -5 | -6 | -6 | -5 | -6 |
MySQL and Decimal
Real-number precision issues also exist in databases.
MySQL provides DECIMAL for exact real-number storage.
In the example below, total precision is 10 including fractional digits, and scale is 2. If omitted, default is precision 10 and scale 0. Maximum precision is 65.
CREATE TABLE `myTable` (
`point` DECIMAL(10, 2) DEFAULT NULL
) ENGINE=InnoDB DEFAULT CHARSET=utf8mb4;