자바에서의 실수(real number)
자바에서 제공하는 실수형 데이터 타입에는 float와 double이 있다. 정수형 int, long 타입과 동일하게 각각
4, 8바이트의 메모리 공간을 사용하지만 실수를 가수와 지수 부분으로 나누어 표현하는 부동 소수점 방식을 기반으로
정수보다 더 넓은 범위의 값을 표현할 수 있다. 참고로 자바에서는 실수 연산에서 double 타입을 기본적으로 사용한다.
소수점 표현 방식
컴퓨터는 노이즈(Noise)로 인하여 2진수 체계를 기반으로 한다. 2진수 표현을 전기적인 신호로 판단하는 것이다. 즉, 신호가 있으면 1, 없다면 0으로 표현한다.
따라서 실수도 2진수로 표현해야 하며, 정수에 비해서 상대적으로 꽤 복잡한 편이다. 실수를 표현하는 방식으로는 고정 소수점 방식(Fixed-Point Number Representation)과 부동 소수점 방식(Floating-Point Number Representation)으로 나눌 수 있다.
고정 소수점 방식
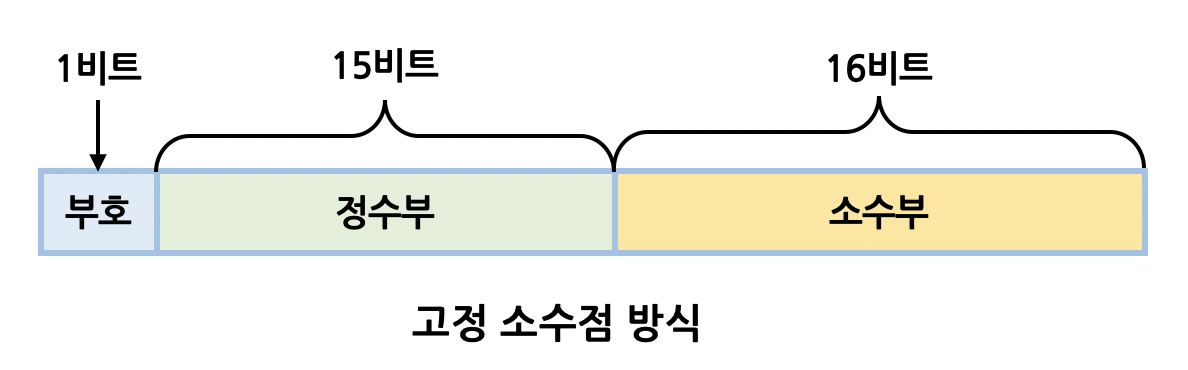
고정 소수점 방식(Fixed-Point Number Representation)은 소수점 이상 또는 소수점 이하를 지정하여 처리하는 방식이다. 즉, 소수부의 자릿수를 정하여 고정된 자릿수의 소수를 표현한다.
맨 앞자리 1자리는 부호 비트로 사용된다. 0이면 양수고, 1이면 음수가 된다. 나머지 자리의 비트들은 소수점을 기준으로 하여 정수부(Integer Part)와 소수부(Fractional Part)로 나뉜다.
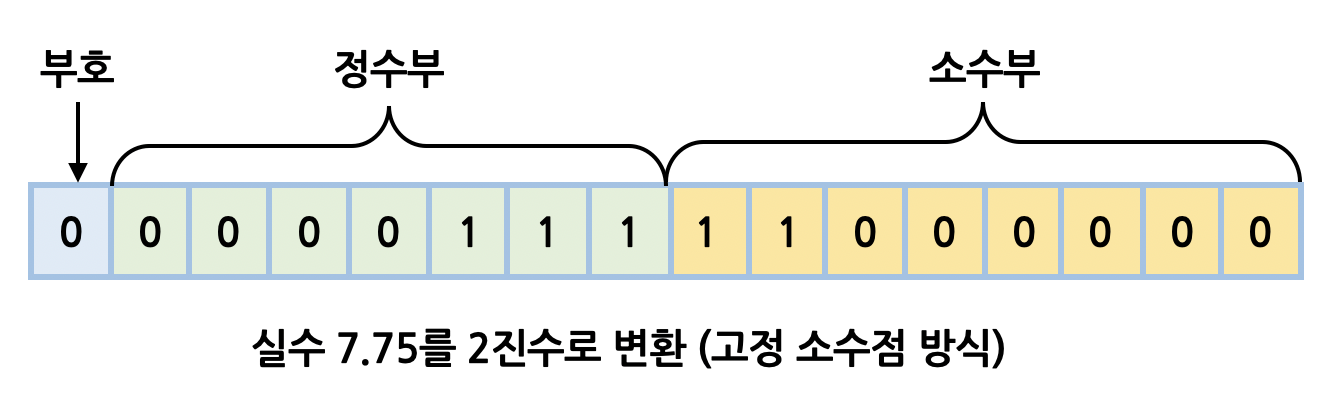
앞서 본 것처럼 고정 소수점 방식은 소수점의 위치를 고정시킨 후 표현하는 것이 특징이다. 예를 들어 7.75라는 실수를 2진수로 변환하면 111.11인데, 고정 소수점 방식으로 표현하면 아래와 같다. 예제는 편의상 16비트 체계를 사용하는 것으로 가정했다.
이처럼 고정 소수점 방식은 제한된 자릿수로 인하여 표현 가능한 실수의 범위와 정밀한 정도가 제한적이기 때문에 잘 사용되지 않는다.
부동 소수점 방식
대부분의 부동 소수점 방식은 IEEE 754 표준을 따르고 있기 때문에, 이 글에서도 이를 기준으로 서술한다.
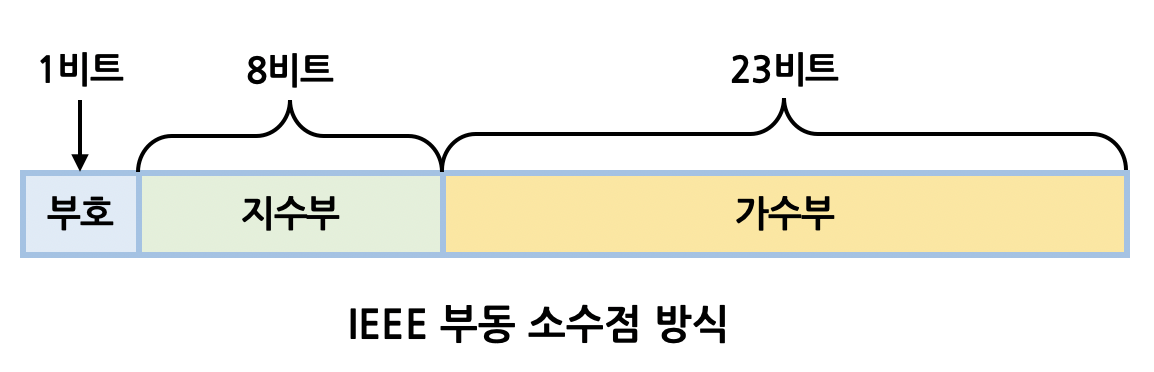
부동 소수점 방식(Floating-Point Number Representation)은 앞서 살펴본 고정 소수점 방식과 조금 다르게 실수를 표현한다. 실수를 부호부(sign), 가수부(Mantissa) 그리고 지수부(Exponent)로 나눈다.
기본 수식으로 \({ (-1) }^{ S }\) x \({ M }\) x \({ 2 }^{ E }\)로 표현할 수 있으며, 각각의 역할은 다음과 같다.
- S: 부호부(Sign) 1비트를 의미하며 0이면 양수고, 1이면 음수가 된다.
- M: 가수부(Mantissa) 23비트를 의미하며, 양의 정수로 표현한다.
- E: 지수부(Exponent) 8비트를 의미하며, 소수점의 위치를 나타낸다.
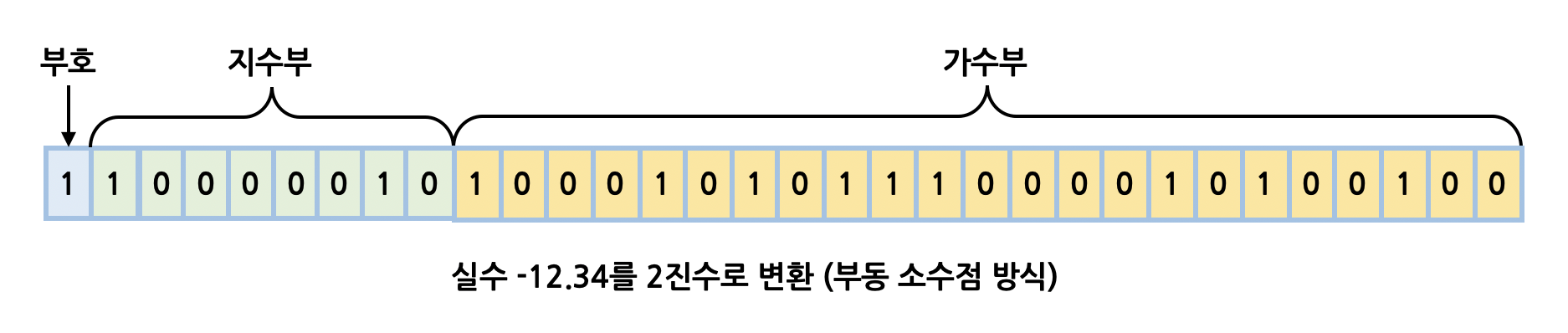
예를 들어, 실수 -12.34를 부동 소수점 방식으로 표현해보면 아래와 같다.
이처럼 부동 소수점 방식은 앞서 살펴본 고정 소수점 방식과 비교했을 때, 상대적으로 훨씬 더 넓은 범위까지 값을 표현할 수 있고 정밀도가 높기 때문에 현재 대부분의 시스템은 부동 소수점 방식으로 실수를 표현한다.
부동 소수점 방식의 오차
앞서 살펴본 것처럼 부동 소수점 방식은 고정 소수점 방식보다 표현할 수 있는 값의 범위가 넓지만, 여전히 정밀도의 문제가 있다. 따라서 실수를 부동 소수점으로 표현하더라도 오차가 존재하는 것을 유의해야 하며, 컴퓨터에서의 실수 표현은 근사값을 표현하는 것으로 이해해야 한다.
다음 예제를 수행해보면 부동 소수점 방식으로 실수를 표현했을 때, 발생할 수 있는 오차를 발견할 수 있다.
double value1 = 12.23;
double value2 = 34.45;
// 46.68 ???
value1 + value2;
12.23와 34.45을 더했으니 결과로 46.68을 예상했겠지만, 실제로는 46.68000000000001가 출력된다. 이와 같이 실수 연산에서는 소수점 단위 값을 정확히 표현하는 것이 아니라 근사값으로 처리하기 때문에 오차가 발생할 수 있다.
근사한 차이지만, 금융 관련 프로그램에서는 이 오차가 큰 영향을 미칠 수 있기 때문에 주의해야 한다. 그러면 이 문제를 어떻게 해결할 수 있을까?
해결책은 BigDecimal
이러한 부동 소수점 표현 방식의 오차를 해결하기 위해 자바에서는 BigDecimal 클래스를 제공하고 있다.
소수점을 다루는 연산을 한다면 BigDecimal 클래스의 사용은 필수적이다.
선언 방법
BigDecimal 클래스는 java.math 패키지 안에 포함되어 있다. 보통 생성자와 파라미터로 문자열을 넘겨 생성하는 것이
기본적이지만, 정적 팩토리 메서드도 제공한다. 생성자를 사용할 때 주의할 점은, 문자열이 아닌 double 타입 값을 넘기면
안 된다.
// 생성자 + 문자열로 초기화하는 방법
BigDecimal value1 = new BigDecimal("12.23");
// double 타입으로 초기화하는 방법
// 내부적으로 생성자 + 문자열을 사용한다.
BigDecimal value2 = BigDecimal.valueOf(34.45);
// 아래와 같이 사용하면 안 된다.
// 12.230000000000000426325641456060111522674560546875
BigDecimal dontDoThis = new BigDecimal(12.23);
사칙연산
더하기(add)
add 메서드로 덧셈 연산을 할 수 있다. 예제에서 사용한 BigDecimal.ONE은 BigDecimal 클래스에서 제공하는 전역 상수다.
ZERO, TEN 도 있다.
BigDecimal value = new BigDecimal("12.23");
// 13.23
value.add(BigDecimal.ONE);
빼기(subtract)
뺄셈 연산은 subtract 메서드를 사용하면 된다.
BigDecimal value = new BigDecimal("12.23");
// 2.23
value.subtract(BigDecimal.TEN);
곱하기(multiply)
곱하기 연산은 multiply 메서드를 사용하면 된다.
BigDecimal value = new BigDecimal("1");
// 10
value.multiply(BigDecimal.TEN);
나누기(divide)
divide 메서드를 사용하면 나눗셈 연산이 가능하다. 하지만 정확하게 나누어 몫이 떨어지지 않는 수의 경우 ArithmeticException 예외를 던진다.
아래 예제를 확인해보자.
BigDecimal value1 = new BigDecimal("11");
BigDecimal value2 = BigDecimal.valueOf(3);
// Exception in thread "main" java.lang.ArithmeticException:
// Non-terminating decimal expansion; no exact representable decimal result.
value1.divide(value2);
아무리 BigDecimal 클래스라도 나누어떨어지지 않는 수는 정확하게 표현할 수 없다. 따라서 divide 메서드를 사용할 때는
소수점 몇 번째짜리까지, 어떻게 처리할 것인지 지정을 해줘야 한다.
예제에서 2번째 파라미터는 N 번째 자리까지 표현할 것인가를 뜻하고, 3번째 파라미터는 처리 방식이다. 즉, 아래 예제의 경우 소수점 3번째 자리에서 반올림하여 2번째 자리까지 표기한다.
참고로 BigDecimal.ROUND_HALF_UP와 같은 상수는 자바 9에서 Deprecated 되었다.
BigDecimal value1 = new BigDecimal("11");
BigDecimal value2 = BigDecimal.valueOf(3);
// 3.67
value1.divide(value2, 2, RoundingMode.HALF_UP);
그 밖의 메서드들
나머지 계산(reminder)
reminder 메서드로 나눗셈 결과의 나머지도 구할 수 있다.
BigDecimal value = new BigDecimal("10");
// 2
value.remainder(BigDecimal.valueOf(4));
값 비교(compareTo)
BigDecimal 인스턴스는 compareTo 메서드를 사용하여 서로 비교할 수 있다. 파라미터로 전달되는 값보다 작은 경우 -1,
큰 경우 1 그리고 같은 경우 0을 반환한다.
BigDecimal value = new BigDecimal("10");
// 0
value.compareTo(BigDecimal.TEN);
// 1
value.compareTo(BigDecimal.ONE);
// -1
BigDecimal.ONE.compareTo(value);
최대, 최소(max, min)
최댓값은 max, 최솟값은 min 메서드를 사용하면 전달되는 파라미터와 비교하여 구할 수 있다.
BigDecimal value = BigDecimal.valueOf(10);
// 10
value.max(BigDecimal.ONE);
// 1
value.min(BigDecimal.ONE);
소수점 처리 방식
자바에서는 BigDecimal 클래스에 다양한 소수점 처리 방식을 제공하고 있다. 몇 가지 예시로 살펴보면 아래와 같다.
// 소수점 첫 번째까지 표현, 두번째 자리에서 반올림
// 12.4
BigDecimal.valueOf(12.35).setScale(1, RoundingMode.HALF_UP);
// 소수점 이하 모두 제거하고 올림
// 13
BigDecimal.valueOf(12.34).setScale(0, RoundingMode.CEILING);
// 음수인 경우는 특정 자릿수 이하 제거
// -12.3
BigDecimal.valueOf(-12.34).setScale(1, RoundingMode.CEILING);
// 특정 자릿수 이하 버림
// 12.3
new BigDecimal("12.37").setScale(1, RoundingMode.FLOOR);
아래는 BigDecimal 클래스에서 제공하는 RoundingMode를 정리한 표이다. 입력값을 기준으로 소수점 첫 번째 자리에서
반올림 모드를 적용한 결과다. 즉, setScale(0, RoundingMode) 형태다.
| 입력 값 | UP | DOWN | CEILING | FLOOR | HALF_UP | HALF_DOWN | HALF_EVEN |
|---|---|---|---|---|---|---|---|
| 5.5 | 6 | 5 | 6 | 5 | 6 | 5 | 6 |
| 2.5 | 3 | 2 | 3 | 2 | 3 | 2 | 2 |
| 1.6 | 2 | 1 | 2 | 1 | 2 | 2 | 2 |
| 1.1 | 2 | 1 | 2 | 1 | 1 | 1 | 1 |
| 1.0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| -1.0 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| -1.1 | -2 | -1 | -1 | -2 | -1 | -1 | -1 |
| -1.6 | -2 | -1 | -1 | -2 | -2 | -2 | -2 |
| -2.5 | -3 | -2 | -2 | -3 | -3 | -2 | -2 |
| -5.5 | -6 | -5 | -5 | -6 | -6 | -5 | -6 |
MySQL과 Decimal
소수점 표현의 오차는 데이터베이스에서도 이어진다. MySQL에서는 실수의 값을 정확하게 표현하기 위해 Decimal이라는 타입을 제공한다.
아래와 같이 지정할 수 있는데, 소수부를 포함한 전체 자릿수는 10이고, 소수부의 자릿수는 2자리를 뜻한다. 지정하지 않는 경우 전체 10자리, 소수부가 없는 0으로 지정된다. 참고로 전체 자릿수의 최대값은 65이다.
CREATE TABLE `myTable` (
`point` DECIMAL(10, 2) DEFAULT NULL
) ENGINE=InnoDB DEFAULT CHARSET=utf8mb4;