Sieve of Eratosthenes?

The Sieve of Eratosthenes derives its name from Eratosthenes, an ancient Greek mathematician who discovered the principle. As the name suggests, it’s about filtering out only prime numbers from natural numbers using a ‘sieve’.

As you can find by searching here and there, there are very many methods for determining prime numbers. There are basic methods of judging one by one directly, and methods of solving using square roots.

So this time, I want to find prime numbers using something a bit unfamiliar called the Sieve of Eratosthenes.

What Method Is It?

First, prime numbers are natural numbers that have only two positive divisors. So numbers like 2, 3, 5, 7, 11 are called prime numbers. Since we’ve also learned about the definition of prime numbers, let’s dig into the Sieve of Eratosthenes!

First, 1 is excluded because it’s not a prime number by the definition of prime numbers. That’s the sieve. Then the remaining numbers become numbers 2 or greater.

Check the smallest number among the remaining numbers. Number 2 remains. Because number 1 was filtered by the sieve earlier! By the definition of prime numbers mentioned earlier, number 2 is a prime number.

Then filter all multiples of 2 with the sieve. That is, filter all even numbers and leave only odd numbers. Now the remaining numbers become numbers 3 or greater.

Again, check the smallest number among the remaining numbers. Number 3 is the smallest. Because numbers 1 and 2 were filtered earlier. Similarly, by the definition of prime numbers, number 3 also becomes a prime number.

Filter all multiples of 3 with the sieve. That is, filter all 3, 6, 9, 12, 15, … etc. Of course, numbers like 6 and 12 are already gone while filtering multiples of number 2.

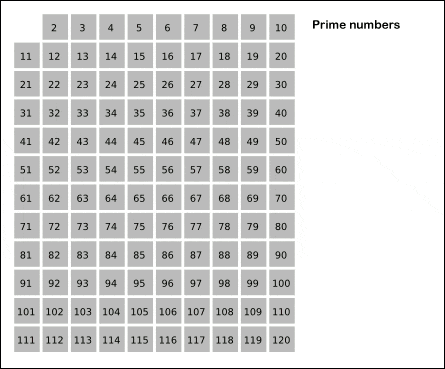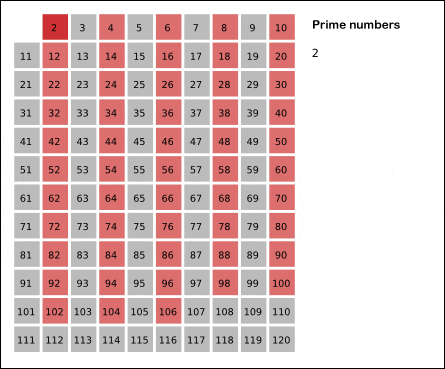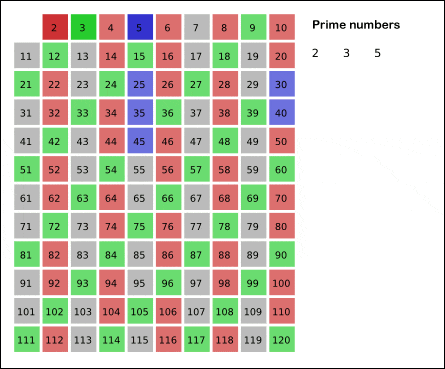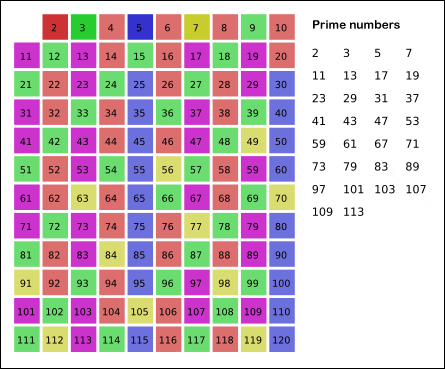
Shall we continue even though it’s tedious? Now the remaining numbers become 5, 7, 11, 13, 17, … etc. and the smallest number is 5. Filter multiples of 5 with the sieve. Then the remaining numbers become 7, 11, 13, 17, … etc. and the smallest number is 7. Filter multiples of 7 with the sieve. Now the remaining numbers become 11, 13, 17, 19, … etc.

Let’s Implement It in Code

Since we’ve examined the principle, implementing it in code now:

#include <stdio.h>
#include <stdlib.h>

#pragma warning(disable:4996)

int main(void)
{
    int maxNumber = 0;
    int *primeArray = NULL;
    int visited = 0;
    int check = 0;
    
    /* Enter maximum value. */
    printf("Enter maximum value : ");
    scanf("%d", &maxNumber);
    
    /* Dynamically allocate. */
    primeArray = (int *)malloc(sizeof(int) * maxNumber);
    if (primeArray == NULL)
    {
        puts("Memory allocation error\n");
        exit(1);
    }
    
    /* Initialize the array allocated above. */
    for (visited = 2; visited <= maxNumber; visited++)
    {
        primeArray[visited] = visited;
    }
    
    /* Apply the Sieve of Eratosthenes. */
    for (visited = 2; visited <= maxNumber; visited++)
    {
        /* Don't check multiples of numbers already checked. */
        if (primeArray[visited] == 0) continue;
        
        for(check = visited * visited; check <= maxNumber; check = check + visited)
        {
            /* Check all those multiples as well. */
            primeArray[check] = 0;
        }
    }
    
    /* Output results. */
    for (visited = 2; visited <= maxNumber; visited++)
    {
        if (primeArray[visited]) printf("%d ", primeArray[visited]);
        if (visited % 10 ==0) printf("\n");
    }
}

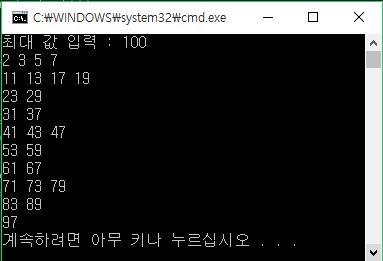
The execution result of the above code is as follows.

What Is the Performance in Finding Prime Numbers?

The time complexity of code applying the Sieve of Eratosthenes becomes \(O(n\log { \log { n } ) }\).

As there are many methods for finding prime numbers, ‘Prime Numbers’ themselves have many interesting aspects. They’re deeply related to long-distance communication, national security, etc., and efforts to find larger prime numbers continue.

Quoting Naver Encyclopedia, it says that the largest prime number discovered so far is a number with 378,632 digits that requires as many as 12 newspaper pages to write.